SMO 算法求解 SVM 拉格朗日系数-工具盒子

之前的 SVM 推导得到了一堆关于拉格朗日系数的表达式，但是没有求解，本文记录 SMO 解决 SMV 问题的思想流程。

SVM 回顾 {#SVM-回顾}

之前经过对 SVM 推导得到了最终需要求解拉格朗日系数的步骤：

$$ \begin{array}{l} \min {\alpha} \frac{1}{2} \sum{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(\Phi\left(x_{i}\right) \cdot \Phi\left(x_{j}\right)\right)-\sum_{i=1}^{n} \alpha_{i}\\ s.t. \sum_{i=1}^{n} \alpha_{i} y_{i}=0 , \alpha_{i} \geq 0 \end{array} $$

其中 $\alpha_i$ 为拉格朗日系数，$y_i$ 为数据标签， $n$ 为数据个数， $x_i$ 为数据向量，$\Phi$ 为核函数映射
仅有 $\alpha_i$ 未知，我们认为 $\alpha_i$ 是有限的，给定一个取值上限 $C$

现在的问题是：如何在满足拉格朗日约束 KKT 条件的同时解出 $\alpha_i$
SMO 算法提供了解决方案

SMO 简介 {#SMO-简介}

SMO (Sequential Minimal Optimization)，翻译过来是序列最小优化算法。算法的核心思想是由于我们需要寻找的是一系列的 $α$ 值使得原始优化问题取极值，但问题是这一系列的值我们很难同时优化 。所以SMO算法想出了一个好办法解决这个问题，把这一系列的 $α$ 中的两个看成是变量 ，其它的全部固定看成是常数 ，通过不断迭代优化这两个变量来优化目标函数。
这里有一个问题是为什么我们要选择两个 $α$ 看成是变量而不选一个呢？选一个不是更加简单吗？因为我们的约束条件当中有一条是 $∑y_iα_i=0$，所以如果我们只选择一个 $α$ 进行调整的话，那么显然会破坏这个约束。所以我们选择两个，其中一个变化，另外一个也随着变化，这样就可以保证不会破坏约束条件了。
为了方便叙述，我们默认选择的两个 $α$ 分别是 $α_1,α_2$。另外由于我们涉及$x_i^Tx_j$的操作，我们令$K_{ij}=x_i^Tx_j$。这样上面的问题可以写成：

$$ \min {\alpha 1, \alpha{2}} \frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} \alpha_{1} \alpha_{2}-\left(\alpha_{1}+\alpha_{2}\right)+y_{1} \alpha_{1} \sum_{i=3}^{m} y_{i} \alpha_{i} K_{i 1}+y_{2} \alpha_{2} \sum_{i=3}^{m} y_{i} \alpha_{i} K_{i, 2}+ Constant $$

其中由于 $y_i=±1$，所以 $y_i^2=1$，上面的 $Constant$ 表示除了$α_1,α_2$ 以外的常数项。我们假设$α_1y_1+α_2y_2=k$，其中 $α_1,α_2∈[0,C]$，由于 $y_i$ 只有两个选项1或者-1，所以我们可以分情况讨论。

核心算法 {#核心算法}

选取样本标注不同 {#选取样本标注不同}

当选取的两个样本标注不同时，$y_1$ 和 $y_2$ 符号不同
由于 $\alpha \geq0$，那么无外乎两种情况之一：
1. $α_1−α_2=k$
2. $α_2−α_1=k$
第一种情况是 $α_2=α_1−k$，第二种情况是 $α_2=α_1+k$。
对于第一种情况，如果 $k < 0$，其实就是第二种情况，同样对于第二种情况，如果 $k > 0$ 其实就是第一种情况，因此 $k$ 的符号正负都可以规约成同一个问题。
这变成了一个线性规划问题，我们把图画出来就非常清晰了。

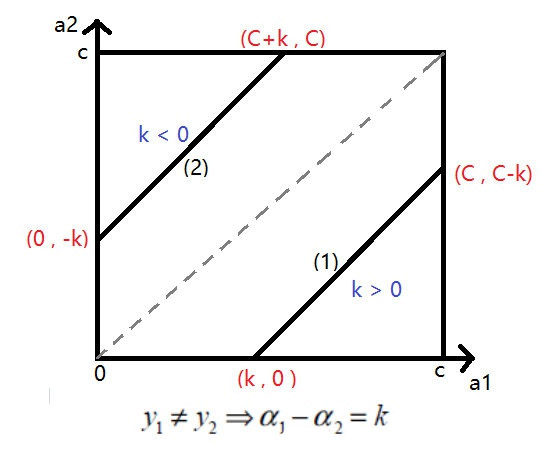
第一种情况，$α_2$ 的范围是 $(0,C−k)$，也就是 $(0,C−\alpha_1+\alpha_2)$
第二种情况，$α_2$ 的范围是$(k, C)$，也就是$(α_2−α_1,C)$。
这里我们把 $k$ 又表示回了 $α_1,α_2$，由于我们要通过迭代的方法来优化 $α_1, α_2$的取值，所以我们令上一轮的$α_1,α_2$分别是$α_{1o},α_{2o}$。这里的 $o$ 指的是 old 的意思
我们把刚才求到的结论综合一下，就可以得到$α_2$下一轮的下界是 $max(0,α_{2o}−α_{1o})$，上界是$min(C+α_{2o}−α_{1o},C)$。

选取样本标注相同 {#选取样本标注相同}

当选取的两个样本标注相同时，$y_1$ 和 $y_2$ 符号相同
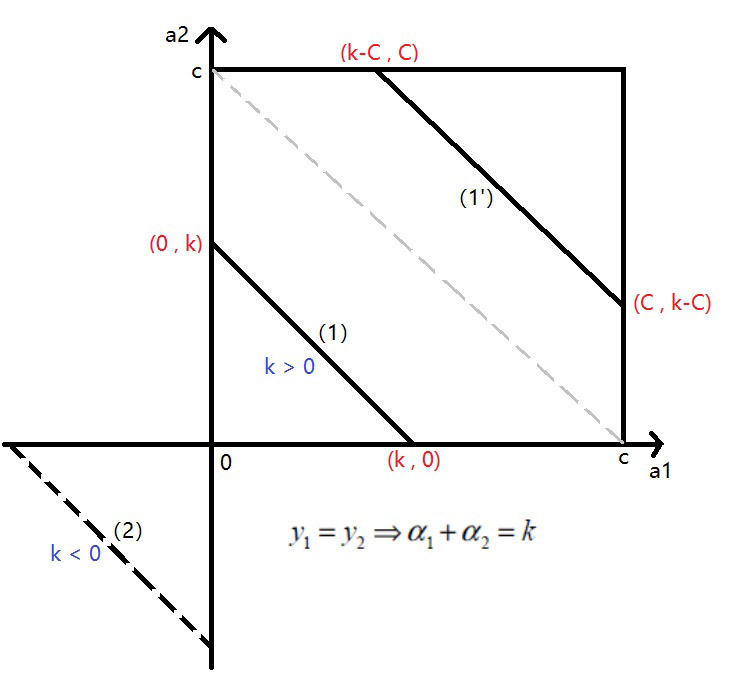
同理，我们画出 $α_1,α_2$ 同号时的情况，也有 $k > 0$ 和 $k < 0$ 两种。

第一种情况是 $y_1=y_2=1$，这时 $α_1+α_2=k$，设 $k > 0$：
- 当 $C > k > 0$：对应的 $α_2$ 的取值是 $(0,k)$，即 $(0,α_{1o}+α_{2o})$
- 当$k > C$，这时候也就是图中 1' 的情况，此时过了中间的虚线，$α_2$ 的范围是 $(k-C,C)$，即 $(α_{1o}+α_{2o}−C,C)$。
第二种情况是 $y_1=y_2=−1$，此时 $α_1+α_2=k$，设 $k < 0$：
- 由于这个时候是不符合约束条件 $0≤α_1,α_2≤C$的，所以此时没有解。
这两种情况综合一下，可以得到下界是 $max(0,α_{1o}+α_{2o}−C)$，上界是 $min(α_{1o}+α_{2o},C)$。

综合求解 $\alpha_2$ {#综合求解-alpha-2}

我们假设我们通过迭代之后得到的下一轮 $α_2$是 $α_{2 new,unc}$，这里的unc是未经过约束的意思。那么我们加上刚才的约束，假设上界为 $H$，下界为 $L$，可以得到：

$$ \alpha_{2 n e w}=\left\{\begin{array}{lr}H & \alpha_{2 n e w, u n c}>H \\ \alpha_{2 n e w, u n c} & L \leq \alpha_{2 n e w, u n c} \leq H \\ L & \alpha_{2 n e w, u n c} < L\end{array}\right. $$

这里的$α_{2new,unc}$是我们利用求导得到取极值时的 $α_2$，但问题是由于存在约束，这个值并不一定能取到。所以上述的一系列操作就是为了探讨约束存在下我们能够取到的极值情况。

代入消元 {#代入消元}

我们现在已经得到了下一轮迭代之后得到的新的 $α_2$ 的取值范围，接下来要做的就是像梯度下降一样，求解出使得损失函数最小的 $α_1$ 和 $α_2$的值，由于 $α_1+α_2$ 的值已经确定，所以我们求解出其中一个即可。
我们令$α_1y_1+α_2y_2=ξ$，那么我们可以代入得到 $α_1=y_1(ξ−α_2y_2)$
我们把这个式子代入原式，得到的式子当中可以消去 $α_1$，这样我们得到的就是只包含 $α_2$ 的式子。我们可以把它看成是一个关于 $α_2$ 的函数，为了进一步简化，我们令v：

$$
v_{i}=\sum_{j=3}^{m} y_{j} \alpha_{j} K i, j, E_{i}=f\left(x_{i}\right)-y_{i}=\sum_{j=1}^{m} \alpha_{j} y_{j} K_{i, j}+b-y_{i}
$$

这里的 $E_i$ 表示的是第 $i$ 个样本真实值与预测值之间的差，我们把上面两个式子代入原式，化简可以得到：

$$
f\left(\alpha_{2}\right)=\frac{1}{2} K_{11}\left(\xi-\alpha_{2} y_{2}\right)+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{2} K_{12}\left(\xi-\alpha_{2} y_{2}\right) \alpha_{2}-\left(\xi-\alpha_{2} y_{2}\right) y_{1}-\alpha_{2}
+\left(\xi-\alpha_{2} y_{2}\right) v_{1}+y_{2} \alpha_{2} v_{2}
$$

接下来就是对这个式子进行求导求极值，就是高中数学的内容了。

$$
\frac{\partial W}{\partial \alpha_{2}}=K_{11} \alpha_{2}+K_{22} \alpha_{2}-2 K_{12} \alpha_{2}-K 11 \xi y_{2}+K 12 \xi y_{2}+y_{1} y_{2}-1-v_{1} y_{2}
+y_{2} v_{2}=0
$$

我们求解这个式子，最终可以得到：

$$
\alpha_{2 \text { new }, \text { unc }}=\alpha_{2 o}+\frac{y_{2}\left(E_{1}-E_{2}\right)}{K_{11}+K_{22}-2 K_{12}}
$$

我们根据这个式子就可以求出 $α_2$ 下一轮迭代之后的值，求出值之后，我们在和约束的上下界比较一下，就可以得到在满足约束的情况下可以取到的最好的值。最后，我们把 $α_2$ 代入式子求解 $α_1$。
这样我们就同时优化了一对 $α$ ，SMO算法其实就是重复使用上面的优化方法不停地选择两个参数进行优化，直到达到迭代次数，或者是不能再带来新的提升为止。
本质上是一种局部参数上的贪心策略，每次调整为局部最优解，以此逐步迭代优化全局问题。