SMV 被广泛用于数据二分类,在变种中也有做异常检测的应用,本文记录异常检测算法 OCSVM(One Class SVM)。
OCSMV 的思想 {#OCSMV-的思想}
-
异常检测是工业领域或应对样本不均衡时的常用方法,训练异常检测模型时往往仅运用 1 类标签数据
-
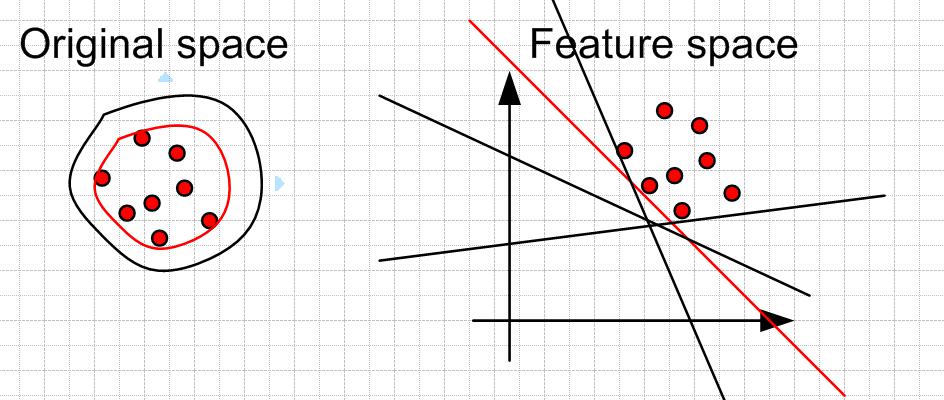
在 SVM 下实现异常检测时也是仅有一类数据,The Support Vector Method For Novelty Detection by Schölkopf et al. 基本上将所有的数据点与零点在特征空间 F 分离开,并且最大化分离超平面到零点的距离。实现的思路是找到一个超平面将所有样本都放在一侧,同时让这个平面距离原点的距离更远
-
也就是找到一个相对于原点来说最"紧致"的平面
-
在测试数据时,在平面远离原点一侧的数据我们认为是同类数据,反之出现在靠近原点一侧的数据则认为是异常数据
优化目标由来 {#优化目标由来}
论文描述的优化目标 {#论文描述的优化目标}
- 在论文中,直接给出了 OCSVM 的优化目标:
$$ \begin{array}{c} \min {w, \zeta{i}, \rho} \frac{1}{2}\|w\|^{2}+\frac{1}{\nu n} \sum_{i=1}^{n} \zeta_{i}-\rho \\ s.t. \left(w^{T} \phi\left(x_{i}\right)\right)>\rho-\zeta_{i}, i=1, \ldots, n \\ \zeta_{i}>0 \end{array} $$
- 其中 $ \zeta_{i} $ 表示松弛变量, $ \nu $ 类似于二分类SVM中的 $ C $,表示正则项系数,用于软 SMV 模型的训练,给训练数据中的异常留个余地
- 论文中并没有叙述这个公式是怎么来的,我按照自己对 SVM 和 OCSVM 的目标的理解尝试做了推导,如有不当烦请指正
直接根据定义推导优化目标 {#直接根据定义推导优化目标}
- 假设我们有 $n$ 个 $m$ 维数据 ${x_1,x_2, ...,x_n},x\in R^m$,都是同一类数据,以此建立 One Class SVM 模型,如果我们暂时不加入松弛变量
- SVM 模型框架不变,目标是寻找一个超平面,在此处我们将超平面方程表示为:
$$
f(x)=w^{T} x- \rho =0
$$
- 既然我们的目的是将现有数据和原点区分开,那么我们不妨假设现有数据标签为 1,那么对样本的约束为:
$$
w^Tx_i-\rho \geq0
$$
- 在满足约束的条件下我们的优化目标是使得原点到平面的几何间隔最大,根据我们已经知道的 SVM 的推导过程,几何间隔为:
$$
\gamma=\frac{f(x)}{||w||}
$$
- 几何间隔是分正负的,此时事实上分为两种情况:
- 如果该平面的位置无论如何都会将原点和数据分到平面的同一侧时,几何间隔非正,要使得几何间隔最大,需要拉近原点和平面的距离
- 如果平面可以将原点和数据分开,此时几何间隔为正,那么就要拉远原点和平面的距离
- 原点到屏幕的几何距离(几何间隔的绝对值)为:
$$
l=\frac{|f(0)|}{||w||}=\frac{|\rho|}{||w||}
$$
-
原点在平面的"数据侧"还是"数据的另一侧"取决于 $\rho$ 的符号:
-
当 $\rho > 0 $ 时:
$$
w^T0-\rho < 0
$$
此时原点和在"数据的另一侧" -
当 $\rho \leq 0 $ 时:
$$
w^T0-\rho \geq 0
$$
此时原点和数据在一起,在"数据侧"
-
-
因此在约束条件下的 $l$,我们的优化目标也分情况讨论:
-
当 $\rho >0$,需要最大化平面到原点的距离,当前优化问题变为:
$$ \begin{array}{c} \max \frac{\rho}{||w||}\\ s.t. w^Tx_i-\rho \geq0,i\in\{1,2,...,n\}\\ \rho >0 \end{array} $$
-
$\rho \leq0$,需要最小化平面到原点的距离,当前优化问题变为:
$$ \begin{array}{c} \max \frac{\rho}{||w||}\\ s.t. w^Tx_i-\rho \geq0,i\in\{1,2,...,n\}\\ \rho \leq 0 \end{array} $$
-
-
这是可以发现,两种情况下的优化目标事实上是相同的,那么我们可以合并两种情况,拿掉对 $\rho$ 的约束,得到原始的 OCSVM 优化目标:
$$ \begin{array}{c} \max \frac{\rho}{||w||}\\ s.t. w^Tx_i-\rho \geq0,i\in\{1,2,...,n\}\\ \end{array} $$
-
很漂亮,但是之后的计算并不容易,因为考虑到 $\rho$ 的符号存在变数,优化目标会纠结:
-
当 $\rho >0$,我们的目标等价于:
$$ \begin{array}{c} \max \rho \\ \min ||w|| \end{array} $$
即:
$$
\min ||w||-\rho
$$-
当 $\rho \leq 0$,我们的目标等价于:
$$ \begin{array}{c} \max \rho \\ \max ||w|| \end{array} $$
即:
$$
\min -||w||-\rho
$$ -
-
这就不好搞了,也和论文中的优化目标相悖
-
由于 $\rho$ 的符号会左右优化目标,按照数据原始样貌训练 OCSVM 很可能难以优化下去
加入松弛变量 {#加入松弛变量}
- 既然直接搞搞不了,论文作者在文中事实上有一句话为问题加了额外的约束:
To separate the data set from the origin, we solve the following quadratic program
- 也就是说这个平面必须将原点和数据分开
- 分不开?咱们加核函数:
$$
\left(w^{T} \phi\left(x_{i}\right)\right)-\rho > 0
$$
- 还分不开?那就加软间隔惩罚项,这回必须保证平面把原点和数据给我分开喽,实在分不开的点就记个账,在优化目标上付点代价假装他分开了:
$$
\left(w^{T} \phi\left(x_{i}\right)\right)>\rho-\zeta_{i}
$$
- 这样的话我们就多了个假设,该超平面已经将原点和数据区分开,那么就强行按照 $\rho >0$ 的情况优化,我们上文讨论过优化目标是:
$$
\min ||w||-\rho
$$
- 等价于:
$$
\min \frac{1}{2}||w||^{2}-\rho
$$
- 再加入软间隔的代价补偿,就得到了原始论文中的优化目标:
$$ \begin{array}{c} \min {w, \zeta{i}, \rho} \frac{1}{2}\|w\|^{2}+\frac{1}{\nu n} \sum_{i=1}^{n} \zeta_{i}-\rho \\ s.t. \left(w^{T} \phi\left(x_{i}\right)\right)>\rho-\zeta_{i}, i=1, \ldots, n \\ \zeta_{i}>0 \end{array} $$
终极纠结 {#终极纠结}
- 我有点死钻牛角尖了,在上述优化目标没有强制加上 $\rho \geq 0$ 的情况下,我认为还是有可能解出 $\rho < 0 $ 的
- 那么一旦这种情况出现,个人认为此时的边界很可能不是最优边界,因为此时正在 $\min ||w||$,平面距离原点的几何距离可能并不会很小,也就是这不是一个包裹住所有数据的最"紧致"平面
求解和 infer {#求解和-infer}
- 求解上述优化函数就可以直接上 SVM 的套路了,原始问题 -> 对偶问题 -> SMO 解拉格朗日乘子 ...
- 推断测试数据时,直接用公式:
$$ f(x)=sign\left(\left(w^{T} \phi\left(x_{i}\right)\right)-\rho\right) =sign( \sum_{i=1}^{n n} \alpha_{i} K\left(x, x_{i}\right)-\rho ) $$
- 负数即为异常样本
Python 实现 {#Python-实现}
引用一位大佬文章的代码:
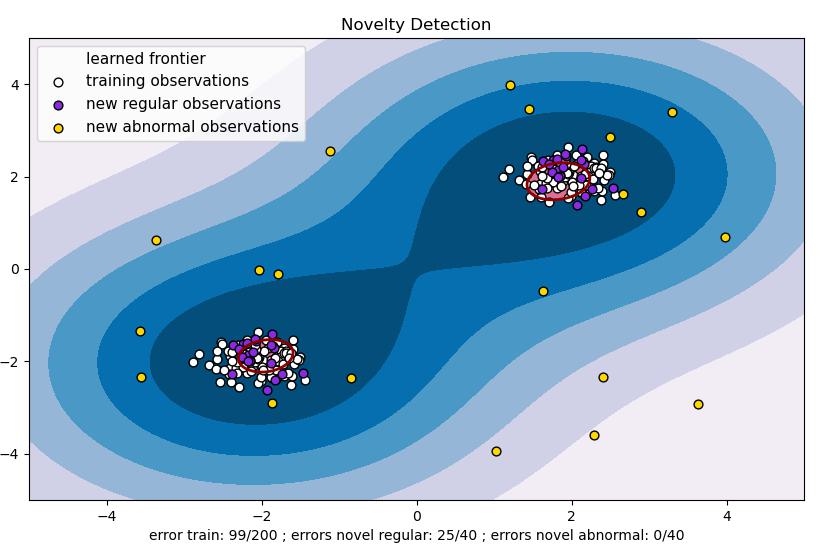
- 核心算法用 sklearn 库实现:
- 运行效果:
原始论文 {#原始论文}
参考资料 {#参考资料}
文章链接:
https://www.zywvvd.com/notes/study/machine-learning/one-class/ocsvm/ocsvm/
 51工具盒子
51工具盒子