# javascript多边形计算库jsclipper的用法 {#javascript多边形计算库jsclipper的用法}
本文讲述javascript多边形计算库jsclipper的用法。jsclipper和同类库比较,功能支持上更完善,且处理效率高,是前端处理多边形计算的首选方案,支持的计算包括多边形的并集、交集、差集、异或、面积、周长等。
# 1. jsclipper涉及的基本概念 {#_1-jsclipper涉及的基本概念}
jsclipper库涉及的基本概念或术语详见文档Clipper库中文文档详解 (opens new window)。
# 1.1 多边形路径描述规则 {#_1-1-多边形路径描述规则}
多边形的路径定义需要严格遵守如下规则,才能准确描述一个多边形:
- 顺时针
按顺时针方向列出路径的顶点。 - 逆时针
按逆时针方向列出路径的顶点。
# 1.2 多边形填充规则 {#_1-2-多边形填充规则}
# 1.2.1 填充规则的定义 {#_1-2-1-填充规则的定义}
因为1个多边形可以由多组路径共同描述(如var subj_paths = [[{X:10,Y:10},{X:110,Y:10},{X:110,Y:110},{X:10,Y:110}], [{X:20,Y:20},{X:20,Y:100},{X:100,Y:100},{X:100,Y:20}]];),所以多边形可以非常复杂。那么多边形填充规则的意义就是为了描述哪些区域是多边形区域的内部,哪些区域是多边形区域的外部。
# 1.2.2 填充规则的分类 {#_1-2-2-填充规则的分类}
jsclipper中支持4种填充规则:
- Even-Odd
奇数次计数的部分被填充,偶数次的部分不填充。 - Non-Zero 所有的非零次计数部分都被填充。
- Positive:所有计数大于零的部分被填充。
- Negative:所有计数小于零的被填充。
# 1.2.3 填充规则计数的定义 {#_1-2-3-填充规则计数的定义}
-
Even-Odd规则中的计数 字面意思是"奇偶"。按该规则,要判断一个点是否在图形内,从该点作任意方向的一条射线,然后检测射线与图形路径的交点的数量。如果结果是奇数则认为点在内部,是偶数则认为点在外部。
可以看出,
Even-Odd规则中的计数与轮廓的方向无关。 -
其它填充规则中的计数 要判断一个点是否在图形内,从该点作任意方向的一条射线,然后检测射线与图形路径的交点情况。从0开始计数,路径从左向右(顺时针)穿过射线则计数加1,从右向左(逆时针)穿过射线则计数减1。
和Even-Odd填充方式不同,其他填充准则中计数会依赖于轮廓方向。
轮廓的方向是由点集的顺序决定的。
# 1.2.4 填充规则的效果图 {#_1-2-4-填充规则的效果图}

注意,该参考图中有个错误,在做计数时,左右方向正好弄反了,导致计数错误。
# 2. 基础示例 {#_2-基础示例}
如下示例演示了jsclipper库的基本用法,包括多边形的并集、交集、差集、异或这4种运算。
<html>
<head>
<title>Javascript Clipper Library / Boolean operations / SVG example</title>
<script src="http://jsclipper.sourceforge.net/6.4.2.2/clipper_unminified.js"></script>
<style>
h3{ margin-bottom:2px}
body,th,td,input,legend,fieldset,p,b,button,select,textarea {
font-size: 14px;
font-family: Arial, Helvetica, sans-serif;
}
</style>
<script>
function draw() {
var subj_paths = [[{X:10,Y:10},{X:110,Y:10},{X:110,Y:110},{X:10,Y:110}],
[{X:20,Y:20},{X:20,Y:100},{X:100,Y:100},{X:100,Y:20}]];
var clip_paths = [[{X:50,Y:50},{X:150,Y:50},{X:150,Y:150},{X:50,Y:150}],
[{X:60,Y:60},{X:60,Y:140},{X:140,Y:140},{X:140,Y:60}]];
var scale = 100;
ClipperLib.JS.ScaleUpPaths(subj_paths, scale);
ClipperLib.JS.ScaleUpPaths(clip_paths, scale);
var cpr = new ClipperLib.Clipper();
cpr.AddPaths(subj_paths, ClipperLib.PolyType.ptSubject, true);
cpr.AddPaths(clip_paths, ClipperLib.PolyType.ptClip, true);
var subject_fillType = ClipperLib.PolyFillType.pftNonZero;
var clip_fillType = ClipperLib.PolyFillType.pftNonZero;
var clipTypes = [ClipperLib.ClipType.ctUnion, ClipperLib.ClipType.ctDifference, ClipperLib.ClipType.ctXor, ClipperLib.ClipType.ctIntersection];
var clipTypesTexts = "Union, Difference, Xor, Intersection";
var solution_paths, svg, cont = document.getElementById('svgcontainer');
var i;
for(i = 0; i < clipTypes.length; i++) {
solution_paths = new ClipperLib.Paths();
console.log("运算前: ", JSON.stringify(solution_paths));
cpr.Execute(clipTypes[i], solution_paths, subject_fillType, clip_fillType);
console.log("运算后: ", JSON.stringify(solution_paths));
svg = '<svg style="margin-top:10px; margin-right:10px;margin-bottom:10px;background-color:#dddddd" width="160" height="160">';
svg += '<path stroke="black" fill="yellow" stroke-width="2" d="' + paths2string(solution_paths, scale) + '"/>';
svg += '</svg>';
cont.innerHTML += svg;
}
cont.innerHTML += "<br>" + clipTypesTexts;
}
// Converts Paths to SVG path string
// and scales down the coordinates
function paths2string (paths, scale) {
var svgpath = "", i, j;
if (!scale) scale = 1;
for(i = 0; i < paths.length; i++) {
for(j = 0; j < paths[i].length; j++){
if (!j) svgpath += "M";
else svgpath += "L";
svgpath += (paths[i][j].X / scale) + ", " + (paths[i][j].Y / scale);
}
svgpath += "Z";
}
if (svgpath=="") svgpath = "M0,0";
return svgpath;
}
</script>
</head>
<body onload="draw()">
<div id="svgcontainer"></div>
</body>
</html>
运算结果如下图:
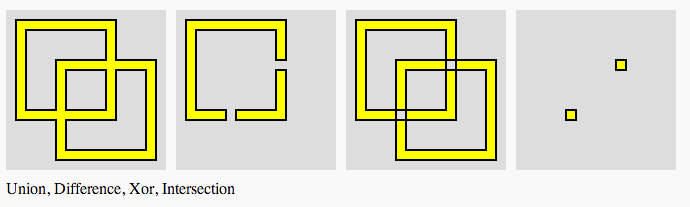
如上代码中的cpr.Execute方法执行完运算操作后,将运算生成的多边形路径信息写入变量solution_paths。控制台打印信息如下:
运算前: []
运算后: [[{"X":11000,"Y":5000},{"X":15000,"Y":5000},{"X":15000,"Y":15000},{"X":5000,"Y":15000},{"X":5000,"Y":11000},{"X":1000,"Y":11000},{"X":1000,"Y":1000},{"X":11000,"Y":1000}],[{"X":11000,"Y":6000},{"X":11000,"Y":11000},{"X":6000,"Y":11000},{"X":6000,"Y":14000},{"X":14000,"Y":14000},{"X":14000,"Y":6000}],[{"X":2000,"Y":2000},{"X":2000,"Y":10000},{"X":5000,"Y":10000},{"X":5000,"Y":5000},{"X":10000,"Y":5000},{"X":10000,"Y":2000}],[{"X":6000,"Y":6000},{"X":6000,"Y":10000},{"X":10000,"Y":10000},{"X":10000,"Y":6000}]]
运算前: []
运算后: [[{"X":11000,"Y":5000},{"X":10000,"Y":5000},{"X":10000,"Y":2000},{"X":2000,"Y":2000},{"X":2000,"Y":10000},{"X":5000,"Y":10000},{"X":5000,"Y":11000},{"X":1000,"Y":11000},{"X":1000,"Y":1000},{"X":11000,"Y":1000}],[{"X":11000,"Y":11000},{"X":6000,"Y":11000},{"X":6000,"Y":10000},{"X":10000,"Y":10000},{"X":10000,"Y":6000},{"X":11000,"Y":6000}]]
运算前: []
运算后: [[{"X":15000,"Y":15000},{"X":5000,"Y":15000},{"X":5000,"Y":11000},{"X":6000,"Y":11000},{"X":6000,"Y":10000},{"X":10000,"Y":10000},{"X":10000,"Y":6000},{"X":11000,"Y":6000},{"X":11000,"Y":5000},{"X":15000,"Y":5000}],[{"X":11000,"Y":6000},{"X":11000,"Y":11000},{"X":6000,"Y":11000},{"X":6000,"Y":14000},{"X":14000,"Y":14000},{"X":14000,"Y":6000}],[{"X":11000,"Y":5000},{"X":10000,"Y":5000},{"X":10000,"Y":6000},{"X":6000,"Y":6000},{"X":6000,"Y":10000},{"X":5000,"Y":10000},{"X":5000,"Y":11000},{"X":1000,"Y":11000},{"X":1000,"Y":1000},{"X":11000,"Y":1000}],[{"X":2000,"Y":2000},{"X":2000,"Y":10000},{"X":5000,"Y":10000},{"X":5000,"Y":5000},{"X":10000,"Y":5000},{"X":10000,"Y":2000}]]
运算前: []
运算后: [[{"X":6000,"Y":11000},{"X":5000,"Y":11000},{"X":5000,"Y":10000},{"X":6000,"Y":10000}],[{"X":11000,"Y":6000},{"X":10000,"Y":6000},{"X":10000,"Y":5000},{"X":11000,"Y":5000}]]
若想了解该示例的详细教程,请前往JavaScript-Clipper.js (opens new window)
# 3. 求面积示例 {#_3-求面积示例}
如下示例演示了如何求1个多边形的面积,以及多个多边形并集的面积。
面积有正、负之分,若以顺时针方向描述顶点路径,则面积为正,若以逆时针方向描述顶点路径,则面积为负。
/**
测试获取多边形面积
*/
function testPolygonArea(){
// path1的面积为400
var path1 = [{X:0,Y:0}, {X:20, Y:0}, {X:20,Y:20}, {X:0, Y:20}];
// path2的面积为10000
var path2 = [{X:150,Y:150},{X:50,Y:150},{X:50,Y:50},{X:150,Y:50}];
// 和path1描述的是同一个路径,只是定点的排列顺序不同
var path1_same = [{X:0, Y:20}, {X:20,Y:20}, {X:20, Y:0}, {X:0,Y:0}];
var area = ClipperLib.JS.AreaOfPolygons([path1]);
console.log("path1的面积", area);
// 因为path1_same以逆时针方向描述顶点, 所以面积为负数
area = ClipperLib.JS.AreaOfPolygons([path1_same]);
console.log("path1_same的面积", area);
// path1的面积+path1的面积,即path1面积的2倍
area = ClipperLib.JS.AreaOfPolygons([path1, path1]);
console.log("path1的面积+path1的面积", area);
// "path1和path1的并集"的面积
area = ClipperLib.JS.AreaOfPolygons(getUnionPaths([path1], [path1]));
console.log("path1和path1的并集的面积", area);
// "path1和path1_same的并集"的面积,可知顶点排列顺序不同(当然无论怎么描述,必须要遵守基本准则: 要么顺时针,要么逆时针),并没有影响并集计算的正确性
area = ClipperLib.JS.AreaOfPolygons(getUnionPaths([path1], [path1_same]));
console.log("path1和path1_same的并集的面积", area);
// "path1和path2的并集"的面积
area = ClipperLib.JS.AreaOfPolygons(getUnionPaths([path1], [path2]));
console.log("path1和path2的并集的面积", area);
// "path1和path2的并集"的面积
area = ClipperLib.JS.AreaOfPolygons(getUnionPaths(getUnionPaths([path1], [path2]), [path1_same]));
console.log("path1和path2的并集的面积", area);
}
/**
获取2个多边形的并集的路径:
注意, path1和path2都是二维数组
*/
function getUnionPaths(path1, path2){
var cpr = new ClipperLib.Clipper();
// 添加裁剪路径
cpr.AddPaths(path1, ClipperLib.PolyType.ptSubject, true);
cpr.AddPaths(path2, ClipperLib.PolyType.ptClip, true);
// 用于保存运算结果
unionPaths = new ClipperLib.Paths();
// 执行运算
cpr.Execute(ClipperLib.ClipType.ctUnion, unionPaths, ClipperLib.PolyFillType.pftEvenOdd, ClipperLib.PolyFillType.pftEvenOdd);
console.log("获取2个多边形的并集的路径, path1:", JSON.stringify(path1));
console.log("获取2个多边形的并集的路径, path2:", JSON.stringify(path2));
console.log("获取2个多边形的并集的路径, 并集路径:", JSON.stringify(unionPaths));
return unionPaths;
}
# 4. 该库可用于cocos creator游戏开发 {#_4-该库可用于cocos-creator游戏开发}
游戏开发中,会经常用到多边形计算,若您是使用cocos creator游戏引擎,则可以使用该库进行多边形计算。
 51工具盒子
51工具盒子