ICP (Iterative Closest Point) 算法是基于 EM(Expectation-maximization algorithm)思想的方法,采用交替迭代法优化得到最优值,本文记录相关内容。
问题描述 {#问题描述}
点云配准(Point Cloud Registration)指的是输入两幅点云 $??$ (source) 和 $??$ (target) ,输出一个变换 $?$ 使得 $?(??)$ 和 $??$ 的重合程度尽可能高。变换 $?$ 可以是刚性的(rigid),也可以不是,本文下面只考虑刚性变换,即变换只包括旋转、平移。
点云配准可以分为粗配准(Coarse Registration)和精配准(Fine Registration)两步。粗配准指的是在两幅点云之间的变换完全未知的情况下进行较为粗糙的配准,目的主要是为精配准提供较好的变换初值;精配准则是给定一个初始变换,进一步优化得到更精确的变换。
图像配准是图像处理研究领域中的一个典型问题和技术难点,其目的在于比较或融合针对同一对象在不同条件下获取的图像,例如图像会来自不同的采集设备,取自不同的时间,不同的拍摄视角等等,有时也需要用到针对不同对象的图像配准问题。具体地说,对于一组图像数据集中的两幅图像,通过寻找一种空间变换把一幅图像映射到另一幅图像,使得两图中对应于空间同一位置的点一一对应起来,从而达到信息融合的目的。 一个经典的应用是场景的重建,比如说一张茶几上摆了很多杯具,用深度摄像机进行场景的扫描,通常不可能通过一次采集就将场景中的物体全部扫描完成,只能是获取场景不同角度的点云,然后将这些点云融合在一起,获得一个完整的场景。
常用方法 {#常用方法}
-
ICP
缺点:
存在多种优化了的变体算法,如八叉树等
-
IDC
-
PIC
-
Point-based probabilistic registration
-
NDT------正态分布变换:
-
Gaussian fields
-
Quadratic patches
-
Likelihood-field matching------随机场匹配
-
CRF匹配
-
Branch-and-bound registration
-
Registration using local geometric features
ICP {#ICP}
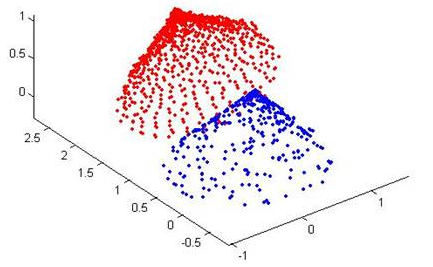
目前应用最广泛的点云精配准算法是迭代最近点算法(Iterative Closest Point, ICP)及各种变种 ICP 算法。ICP 算法是一种点集对点集配准方法。如下图所示,PR(红色点云)和RB(蓝色点云)是两个点集,该算法就是计算怎么把PB平移旋转,使PB和PR尽量重叠。
ICP算法本质上是基于最小二乘法的最优配准方法。该算法重复进行选择对应关系点对, 计算最优刚体变换,直到满足正确配准的收敛精度要求。算法的目的是要找到待配准点云数据与参考云数据之间的旋转参数R和平移参数 T,使得两点数据之间满足某种度量准则下的最优匹配。
ICP 算法描述 {#ICP-算法描述}
对于 $?$ 是刚性变换的情形,点云配准问题可以描述为: $$ \begin{equation} R^{\ast}, t^{\ast} = \mathop{\arg\min}{R, t} \frac{1}{|P_s|} \sum{i=1}^{|P_s|} || p_t^i - (R \cdot p_s^i + t) ||^2 \end{equation} $$
这里 $?_?$ 和 $p_t$ 是源点云和目标点云中的一一对应点。
ICP 算法的直观想法如下:
- 如果我们知道两幅点云上点的对应关系,那么我们可以用 Least Squares 来求解 R, t 参数;
- 怎么知道点的对应关系呢?如果我们已经知道了一个大概靠谱的 R, t 参数,那么我们可以通过贪心的方式找两幅点云上点的对应关系(直接找距离最近的点作为对应点)。
ICP 算法实际上就是交替进行上述两个步骤,迭代进行计算,直到收敛。
ICP 一般算法流程为:
- 点云预处理
- 滤波、清理数据等
- 匹配
- 应用上一步求解出的变换,找最近点
- 加权
- 调整一些对应点对的权重
- 剔除不合理的对应点对
- 计算 loss
- 最小化 loss,求解当前最优变换
- 回到步骤 2. 进行迭代,直到收敛
整体上来看,ICP 把点云配准问题拆分成了两个子问题:
- 找最近点
- 找最优变换
找最近对应点(Find Closet Point) {#找最近对应点(Find-Closet-Point)}
利用初始 $R_0$、$?0$ 或上一次迭代得到的 $R{k−1}$、$t_{k−1}$ 对初始点云进行变换,得到一个临时的变换点云,然后用这个点云和目标点云进行比较,找出源点云中每一个点在目标点云中的最近邻点。
如果直接进行比较找最近邻点,需要进行两重循环,计算复杂度为 $O(|P_s|⋅|P_t|) $,这一步会比较耗时,常见的加速方法有:
- 设置距离阈值,当点与点距离小于一定阈值就认为找到了对应点,不用遍历完整个点集;
- 使用 ANN(Approximate Nearest Neighbor) 加速查找,常用的有 KD-tree;KD-tree 建树的计算复杂度为
O(N log(N)),查找通常复杂度为O(log(N))(最坏情况下O(N))。
求解最优变换(Find Best Transform) {#求解最优变换(Find-Best-Transform)}
对于 point-to-point ICP 问题,求最优变换是有闭形式解(closed-form solution)的,可以借助 SVD 分解来计算。
先给出结论,在已知点的对应关系的情况下,设 $\bar p_s$, $\bar p_t$ 分别表示源点云和目标点云的质心,令 $\hat p_s^i = p_s^i - \bar p_s$,$\hat p_t^i = p_t^i - \bar p_t$ ,令: $$ H = \sum_{i=1}^{|P_s|} {\hat p_s^i} {\hat p_t^i}^T $$ 这是一个 $3 \times3$ 矩阵,对 H 进行 SVD 分解得到 $H = U \Sigma V^T$ ,则 point-to-point ICP 问题最优旋转为: $$ \begin{equation} R^{\ast} = V U^T \end{equation} $$ 最优平移为: $$ \begin{equation} t^{\ast} = \bar p_t - R^{\ast} \bar p_s \end{equation} $$ 下面分别给出证明。
计算最优平移 {#计算最优平移}
令 $N = |P_s|$ ,设 $F(t) = \sum_{i=1}^{N} ||(R \cdot p_s^i + t) - p_t^i||^2$ ,对其进行求导,则有: $$ \begin{equation} \begin{aligned} \frac{\partial F}{\partial t} &= \sum_{i=1}^{N} 2 (R \cdot p_s^i + t - p_t^i) \\ &= 2nt + 2R\sum_{i=1}^{N}p_s^i - 2\sum_{i=1}^{N}p_t^i \end{aligned} \end{equation} $$ 令导数为 0 ,则有: $$ \begin{equation} \begin{aligned} t &= \frac{1}{N} \sum_{i=1}^{N} p_t^i - R \frac{1}{N} \sum_{i=1}^{N} p_s^i \\ &= \bar p_t - R \bar p_s \end{aligned} \end{equation} $$
无论 R 取值如何,根据上式我们都可以求得最优的 t,使得 loss 最小。下面我们来推导最优旋转的计算公式。
计算最优旋转 {#计算最优旋转}
经过最优平移的推导,我们知道无论旋转如何取值,都可以通过计算点云的质心来得到最优平移,为了下面计算上的简便,我们不妨不考虑平移的影响,先将源点云和目标点云都转换到质心坐标下,这也就是之前令 $\hat p_s^i = p_s^i - \bar p_s$ , $\hat p_t^i = p_t^i - \bar p_t$ 的意义。
下面我们用 $\hat p_s^i$ 和 $\hat p_t^i$ 进行推导。
不考虑平移,则 loss 可以写成: $$ \begin{equation} F(R) = \sum_{i=1}^{N} ||R \cdot \hat p_s^i - \hat p_t^i||^2 \end{equation} $$ 先化简 $||R \cdot \hat p_s^i - \hat p_t^i||^2$: $$ \begin{equation} \begin{aligned} ||R \cdot \hat p_s^i - \hat p_t^i||^2 &= (R \cdot \hat p_s^i - \hat p_t^i)^T(R \cdot \hat p_s^i - \hat p_t^i) \\ &= ({\hat p_s^i}^T R^T - {\hat p_t^i}^T)(R \cdot \hat p_s^i - \hat p_t^i) \\ &= {\hat p_s^i}^T R^T R {\hat p_s^i} - {\hat p_t^i}^T R {\hat p_s^i} - {\hat p_s^i}^T R^T {\hat p_t^i} + {\hat p_t^i}^T {\hat p_t^i} \\ &= ||{\hat p_s^i}||^2 + ||{\hat p_t^i}||^2 - {\hat p_t^i}^T R {\hat p_s^i} - {\hat p_s^i}^T R^T {\hat p_t^i} \\ &= ||{\hat p_s^i}||^2 + ||{\hat p_t^i}||^2 - 2{\hat p_t^i}^T R {\hat p_s^i} \end{aligned} \end{equation} $$ 这里利用到了 $R^T R = I$ 和 ${\hat p_t^i}^T R {\hat p_s^i} = {\hat p_s^i}^T R^T {\hat p_t^i}$ (标量的转置等于自身)的性质。
由于点的坐标是确定的(和 R 无关),所以最小化原 loss 等价于求: $$ \begin{equation} R^{\ast} = \mathop{\arg\min}{R} (-2 \sum{i=1}^{N} {\hat p_t^i}^T R {\hat p_s^i}) \end{equation} $$ 也即为求: $$ \begin{equation} R^{\ast} = \mathop{\arg\max}{R} (\sum{i=1}^{N} {\hat p_t^i}^T R {\hat p_s^i}) \end{equation} $$ 注意到 $\sum_{i=1}^{N} {\hat p_t^i}^T R {\hat p_s^i} = trace(P_t^T R P_s)$ (由矩阵乘法及 trace 的定义可得) 则问题转化为: $$ \begin{equation} R^{\ast} = \mathop{\arg\max}{R} trace(P_t^T R P_s) \end{equation} $$ 根据 trace 的性质 $trace(AB)=trace(BA)$,(这里不要求 A, B 为方阵,只要 $A*B$ 是方阵即可),有: $$ \begin{equation} trace(P_t^T R P_s) = trace(R P_s P_t^T) \end{equation} $$ 还记得前面定义的矩阵 H 和其 SVD 分解吗?带入上式得到: $$ \begin{equation} \begin{aligned} trace(P_t^T R P_s) &= trace(R P_s P_t^T) \\ &= trace(R H) \\ &= trace(R U \Sigma V^T) \\ &= trace(\Sigma V^T R U) \end{aligned} \end{equation} $$ 注意这里 $?,?,?$ 都是正交矩阵(orthogonal matrices),所以 $V^T R U$ 也是正交矩阵。令 $$ M = V^T R U = \left[ \begin{array}{cccc} m{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{array} \right] $$ 则有: $$ \begin{equation} \begin{aligned} trace(\Sigma V^T R U) &= trace(\Sigma M) \\ & = \sigma_1 m_{11} + \sigma_2 m_{22} + \sigma_1 m_{33} \end{aligned} \end{equation} $$ 根据奇异值非负的性质和正交矩阵的性质(正交矩阵中的元素绝对值不大于 1),容易证得只有当 ? 为单位阵时 $trace(ΣM)$ 最大,即: $$ \begin{equation} \begin{aligned} V^T R U = I \\ R = V U^T \end{aligned} \end{equation} $$ 所以有 $R^{\ast} = V U^T$。 最后还需要进行 Orientation rectification,即验证 $R^{\ast} = V U^T$ 是不是一个旋转矩阵(检查是否有 $|R|=1$),因为存在 $|R|=−1$ 的可能,此时 $?$ 表示的不是旋转而是一个 reflection,所以我们还要给上述优化求解加上一个 $|R|=1$ 的约束。 根据矩阵行列式的性质,以及 $U, V$ 都是正交阵: $$ \begin{equation} \begin{aligned} |M| &= |V^T| |U| |R| \\ &= |V^T| |U| = \pm 1 \end{aligned} \end{equation} $$
如果 $|VU^T|=1$,则 $|M|=1$, $R^∗=VU^T$ 已经给出最优旋转;如果 $|VU^T|=−1$,则 $|M|=−1$,我们需要求解此时的 $?$,也就是分析 $M$ 应该具有何种形式。具体的讨论请参考这里,本文直接给出结论:当 $|M|=−1$ 时,使得 $?????(Σ?) $ 最大的 $?$ 为: $$ \begin{equation} M = \left[ \begin{array}{cccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{array} \right] \end{equation} $$ 综合考虑 $|M|=1$ 和 $|M|=−1$ 两种情况,我们可以得到: $$ \begin{equation} R^{\ast} = V \left[ \begin{array}{cccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & |V U^T| \end{array} \right] U^T \end{equation} $$
简单总结一下求解最优变换的步骤:
- 计算源点云和目标点云质心;
- 将源点云和目标点云转换到质心坐标系;
- 计算矩阵 H(形式类似"协方差矩阵");
- 对 H 求 SVD 分解,根据公式求得 $?^∗$;
- 根据公式计算 $?^∗$。
迭代 {#迭代}
每一次迭代我们都会得到当前的最优变换参数 $R_k,t_k$ ,然后将该变换作用于当前源点云;"找最近对应点"和"求解最优变换"这两步不停迭代进行,直到满足迭代终止条件,常用的终止条件有:
- $R_k,t_k$ 的变化量小于一定值
- loss 变化量小于一定值
- 达到最大迭代次数
ICP 的优缺点及一些改进算法 {#ICP-的优缺点及一些改进算法}
ICP 优点:
- 简单,不必对点云进行分割和特征提取
- 初值较好情况下,精度和收敛性都不错
ICP 缺点:
- 找最近对应点的计算开销较大
- 只考虑了点与点距离,缺少对点云结构信息的利用
原始的 ICP 算法计算开销大,对初始变换敏感,容易陷入局部最优解。自 ICP 提出以来,有相当多的 ICP 改进算法,简要列举一些:
- Point-to-Plane ICP,原始 ICP 算法的代价函数中使用的 point-to-point 距离,point-to-plane 则是考虑源顶点到目标顶点所在面的距离,比起直接计算点到点距离,考虑了点云的局部结构,精度更高,不容易陷入局部最优;但要注意 point-to-plane 的优化是一个非线性问题,速度比较慢,一般使用其线性化近似;
- Plane-to-Plane ICP,point-to-plane 只考虑目标点云局部结构, plane-to-plane 顾名思义就是也考虑源点云的局部结构,计算面到面的距离;
- Generalized ICP (GICP),综合考虑 point-to-point、point-to-plane 和 plane-to-plane 策略,精度、鲁棒性都有所提高;
- Normal Iterative Closest Point (NICP),考虑法向量和局部曲率,更进一步利用了点云的局部结构信息,其论文中实验结果比 GICP 的性能更好。
实际使用中的一些注意事项 {#实际使用中的一些注意事项}
- ICP 比较依赖于变换初值,平移比较简单,直接用点云质心来估计;旋转初值的话可以手动调一个粗略值,或者沿每个轴的旋转进行采样、组合来尝试(不适合实时性应用);
- 点太多的话可以先降采样;
- 找到一些 anchor 点对(比如先用特征点匹配),可以帮助加速收敛;
- 对应用场景引入一些合理假设,比如限制旋转、平移的范围,变换自由度数量等。
参考资料 {#参考资料}
- https://yilingui.xyz/2019/11/20/191120_point_cloud_registration_icp/
- https://www.cnblogs.com/sddai/p/6129446.html
- https://www.cnblogs.com/21207-iHome/p/6038853.html
 51工具盒子
51工具盒子