最大流最小割算法-工具盒子

最大流最小割（maxflow-mincut）是图像分割的经典算法之一，同时也在"Graph Cut"、"Grab Cut"等算法中都有被使用过。本文记录相关算法。

简介 {#简介}

最大流最小割算法是图像分割的经典算法之一，同时也在"Graph Cut"、"Grab Cut"等算法中都有被使用过。
最小割最大流算法是指在一个有向的图中，能够从源点（source）到达汇点（terminal）的最大流量等于如果从图中剪除就能够导致网络流中断的边的集合的最小容量和。即在任何网络中，最大流的值等于最小割的容量。
原始论文：《Interactive Graph Cuts for Optimal Boundary & Region Segmentation of Objects in N-D Images》

核心概念 {#核心概念}

最大流最小割算法设计一些图论的概念，以一个简单的图为例，介绍一些概念

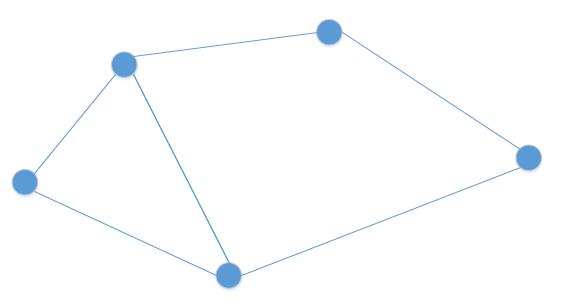
割 {#割}

将一个图的节点分为两种，切割的方法就是割，两种节点之间的连接线组成的集合叫做割集

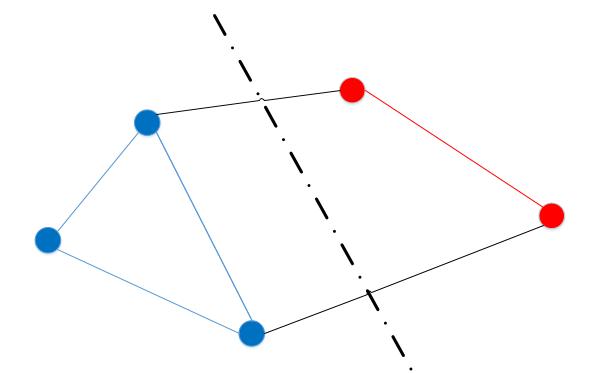
需要说明的是，切割分开的节点不必相连，举例如图下图所示，也是一个合法的割

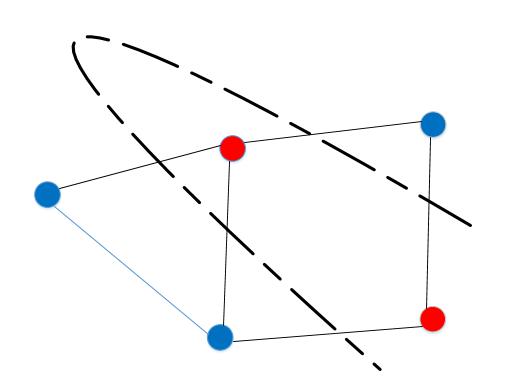
最小割 {#最小割}

图的最小切割是其在某种意义上是最小的切割。图的最小割可以分很多情况进行讨论，例如有向图、无向图，边的权重等。

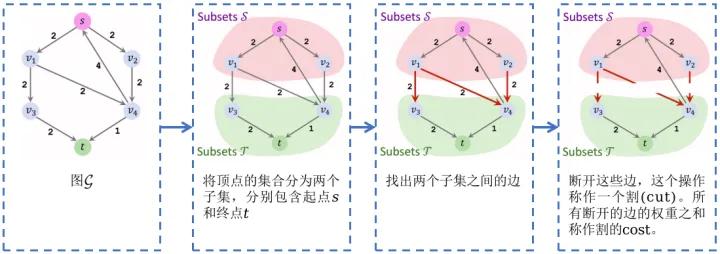
对于无权重图来说，割为将 $S$ 到 $T$ 彻底分割开的断掉边数量最少的割
下图是一张无向无权重图和它的两个割，红色的线格割掉了三条边，而绿色的线割掉了两条边，很明显绿色的线为该图的最小割。

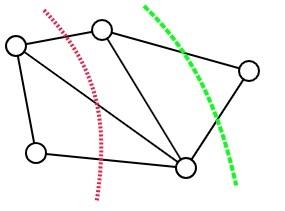
如下图所示，是一个有向带权图，共有4个顶点和5条边。每条边上的箭头代表了边的方向，每条边上的数字代表了边的权重。

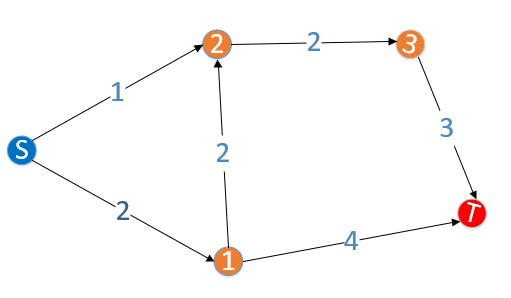
最小割指的是是割集权重最小的割

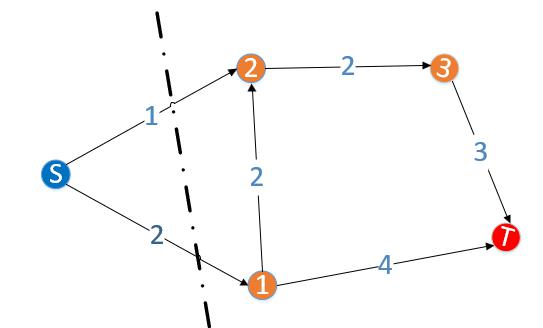
流 {#流}

有向有权图中，假设 $S$ 是一个一直出水的源头，有向边可以从源头按照自己的方向流水，非源头节点输出的水量不大于输入的水量，每条边流过的水量不大于边的权重，每一个从 $S$ 到 $T$ 节点送水的方案为一个流，$T$ 收到的总水为这个流的水量

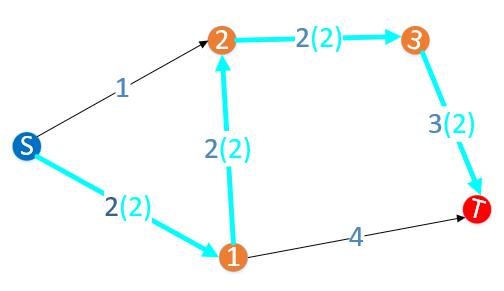
上图浅蓝色线条为流水方案，路径与水量用 S->1->2->3->T:2 表示，但显然这个并不是流量最大的流。

最大流 {#最大流}

在确定的向有权图中，由 $S$ 到 $T$ 的水量最大的流为最大流

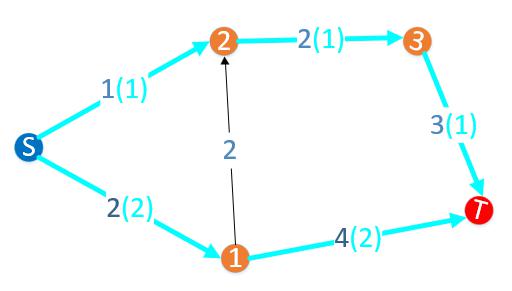
最大流 Ford-Fulkerson 算法 {#最大流-Ford-Fulkerson-算法}

初始化，所有边的flow都初始化为0

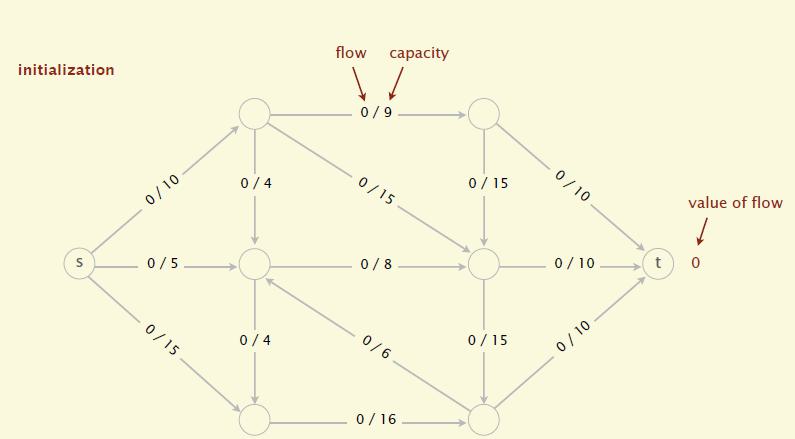
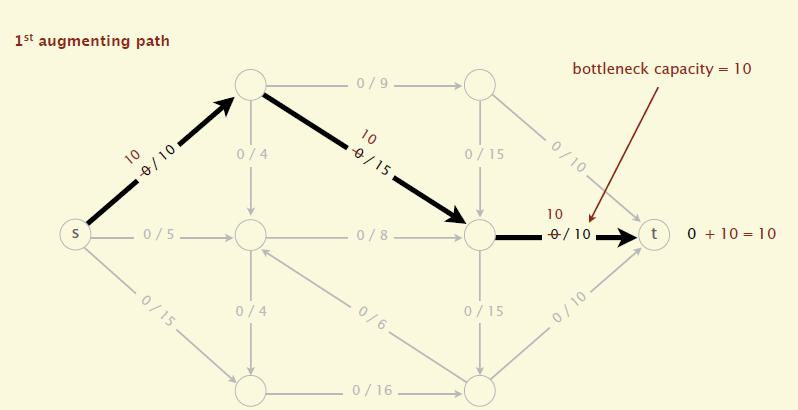
沿着增广路径增加flow。增广路径是一条从 $s$ 到 $t$ 的无向路径，但也有些条件，可以经过没有满容量的前向路径（$s$ 到 $t$）或者是不为空的反向路径( $t$ -> $s$)

核心思路在于用深度优先或广度优先搜索增广路径时提供反向流水（反悔）的可能

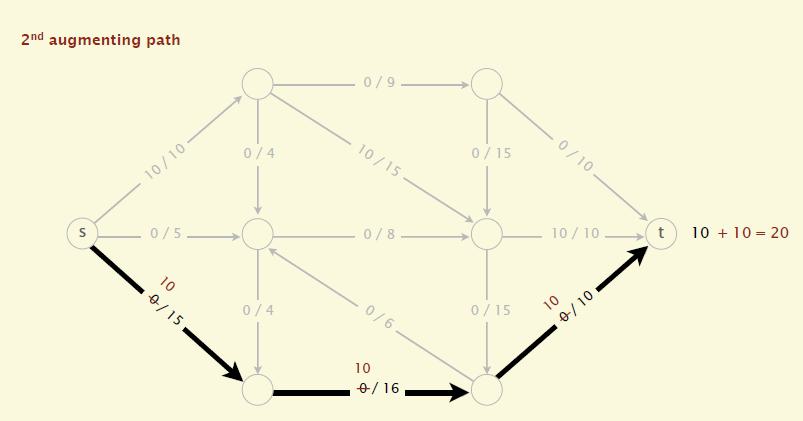
已经"流水"的路径可以"反悔"，而且过程中仍然保持着流的合理性。

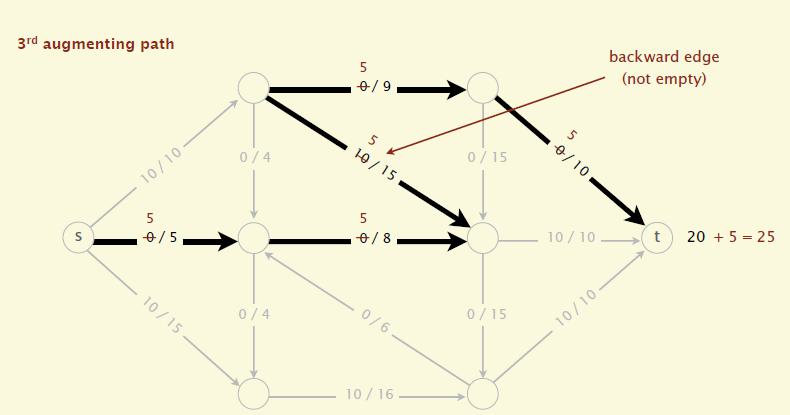
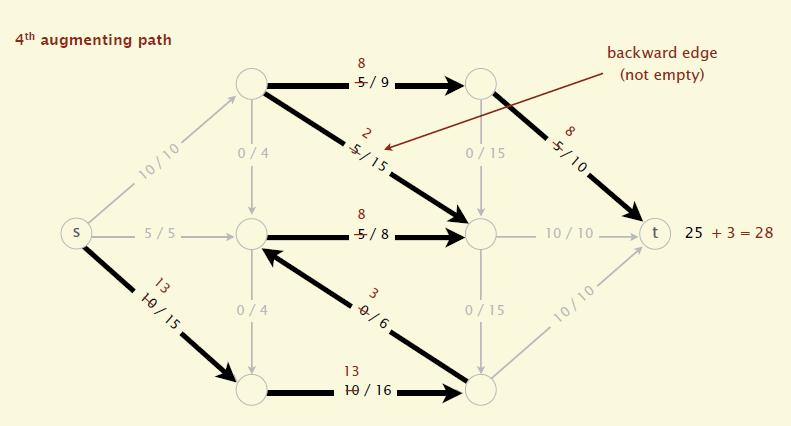
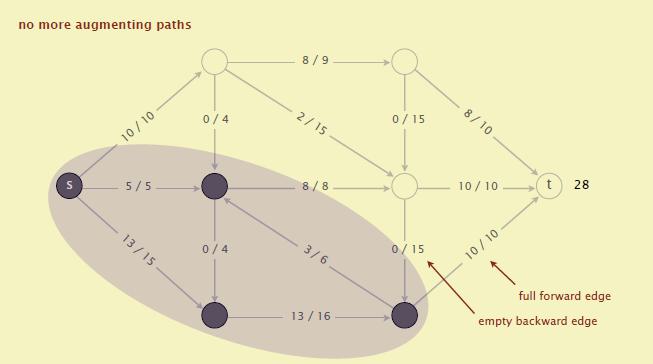
在找不到更多增广路径时就完成了最大流的搜索算法

最大流 Yuri Boykov算法 {#最大流-Yuri-Boykov算法}

假设以源点s和汇点t在图结构上构造两颗没有交集的树，分别为树S和树T，如下图所示。树S中的所有边都是由父节点指向子节点（存在流量），树T中则由子节点指向父节点。不在两树中的节点为"自由"状态。搜索树S和T中的节点只有两种状态："主动"和"被动"。主动态的节点表示搜索树的外边界节点，意思是从该节点出发还可以扩展搜索树，而被动态节点表示搜索树内部的节点，树不能由该节点向外扩展。主动态节点因为可以向外扩展，所以有可能会搜索到另一搜索树的节点，当主动节点检测到另一搜索树的节点，就找到了一条增广路径。
Yuri提出的算法主要循环以下三个步骤：
1. "增长"阶段：搜索树S和T扩展节点，直到两树相遇，得到一条由源点s到汇点t的增广路径。
2. "增广"阶段：根据找到的增广路径将搜索树拆分为子树或森林。
3. "领养"阶段：搜索树S和T重新构建。
初始化

初始化时，搜索树S只有源点s为主动节点，搜索树T只有汇点t作为主动节点，增长搜索树直到它们的主动节点相遇，得到一条增广路径P。如果P为空则算法终止，反之则对P进行增广流量处理。然后对孤点进行领养处理，以此循环。
增长阶段

主动态节点搜索相邻且邻边仍有可用流量的自由节点作为搜索树新的子节点，新增长的子节点又称为该搜索树的主动态节点，搜索树继续扩展增长。当主动态节点的所有邻点都检测过，主动态节点变为被动态节点。当两颗搜索树的主动态节点搜索到对方的节点时，增长阶段终止。然后根据当前建树情况，找到一条增广路径。
增广阶段

这个阶段根据增长阶段找到的增广路径进行增广流量统计，即求出经过该路径的最大流量，意味着路径中至少有一条边达到饱和态，也就是所经流量等于该边的流量值。因此搜索树S和T中会出现一种新的节点，称为"孤点"（orphans），意思就是连接它与其父节点的边已达饱和态，没有流可以再到达这个节点。

所以在增广阶段搜索树S和T可能会拆分为多棵子树，从而形成森林。源点s和汇点t仍充当两颗子树的根节点，而孤点成为其余子树的根节点。

首先找到路径P的瓶颈值，即最小流量边，为该路径的最大流量值。流量经过后，路径P中至少有一条边变为饱和态，即所经流量等于自身流量值，该边连接的子节点变为孤点。
领养阶段

领养阶段字面上理解就能看出是针对孤点进行处理的阶段，该阶段也是为了恢复搜索树S和T的单一性，即图中除了两颗搜索树，其余节点都归为主动态、被动态和自由态，消除孤点。做法是为每个孤点找到一个新的合法父节点，该父节点原来必须与孤点属于同一搜索树，而且父节点与孤点间有一条未饱和（仍有可经流量）的边。若没有符合要求的父节点，该孤点变为自由节点。以此处理所有孤点和孤点的子节点。当所有孤点都处理后，领养阶段结束，最终只剩下原有的搜索树S和T。

最大流的求解过程就是循环重复以上三个阶段，直到搜索树S和T不能再增长。

最大流和最小割的关系 {#最大流和最小割的关系}

最大流最小割定理 {#最大流最小割定理}

任意一个图中，从起点 $S$ 到终点 $T$ 的最大流的流量，等于分离起点 $S$ 和终点 $T$ 的最小割的容量。

等价简要证明 {#等价简要证明}

最大流不可能大于最小割

因为最大流所有的水流都一定经过最小割那些割边，流过的水流怎么可能比水管容量还大呢？
最大流不可能小于最小割

如果小，那么说明水管容量没有物尽其用，可以继续加大水流。

由此可见，最大流和最小割是等价的，是在求解同一个问题。
在求解最小割时往往会转换成最大流的求解。

对偶证明 {#对偶证明}

首先定义一个概念 $net\ flow$,经过一个割 $cut(A,B)$ 的 $net\ flow$ 等于从 $A$ 到 $B$ 的边 flow 的和减去从 $B$ 到 $A$ 边 $flow$ 的和。
然后我们就有了 $flow\ value$ 引理：$f$ 为任意的流，$cut(A,B)$ 为任意的割，那么 $f$ 的值 $flow\ value $（也就是 $t$ 的 $inflow$）等于经过 $cut(A,B)$ 的 $net\ flow$.
如下图，$value\ of\ flow = 8+9+10 = 27$ ,而割的 $net\ flow = 8+2+7-2+12 = 27$.要证明这个引理可以用数学归纳法。

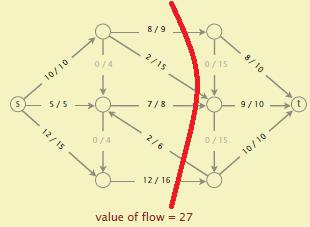
Weak duality(弱对偶)：$f$ 为任意的流，$cut(A,B)$ 为任意的割，那么 $Value\ of\ flow <= capacity\ of\ cut(A,B)$
因为 $cut(A,B)$ 等于从 $A$ 到 $B$ 流量，而 $value\ of\ flow$ 等于 $cut(A,B)$ 的 $net\ flow$, 还得减去从$B$ 到 $A$ 边的流量。

那么现在我们可以引出两个定理：

增广路径定理 （Augmenting Path theorem）: 一个流 $f$ 是最大流当且仅当没有增广路径。
最小割最大流定理 （Maxflow-mincut theorem）: Maxflow 的值等于最小割的容量。

要证明上面的定理，只要证明下面三个条件是等价的就可以了：

存在一个割的容量等于$flow\ f$ 的值
$f$ 是最大流
对于$f$没有增广路径

等价证明 {#等价证明}

首先我们证明 1->2。假设我们有一个割 $cut(A,B)$ 的容量等于 $f$ 的值，那么利用弱对偶的关系，其他流的值<= $cut(A,B)$ 的容量，而由于 1 的假设，$cut(A,B)$ 的容量等于 $f$ 的值，因此得到其他流的值都小于 $f$ 的值，从而 2 成立
接着证明 2->3。我们来证明它的逆否命题。对于 $f$ 如果还有增广路径，那$f$不是最大流 ，这很显然，如果按照 Ford-Fulkerson 算法的话，我们还可以增加 flow f 的值，因此 $f$ 就不会是最大流，因此逆否命题成立，也就代表 2->3成立。
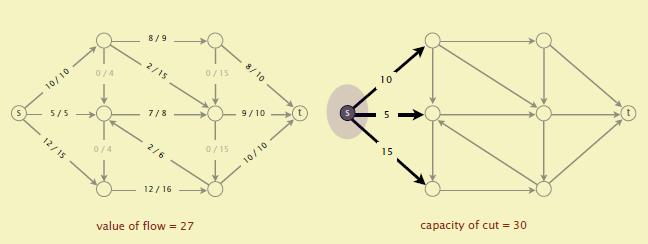
最后证明从 3->1。让割 $cut(A,B)$ 满足这么一个条件：$s$ 在 $A$ 中，且 $A$ 中的顶点通过一些无向的边连接而成，这些边要么是不是满的前向边要么是非空的反向边。如下图中加粗的边。

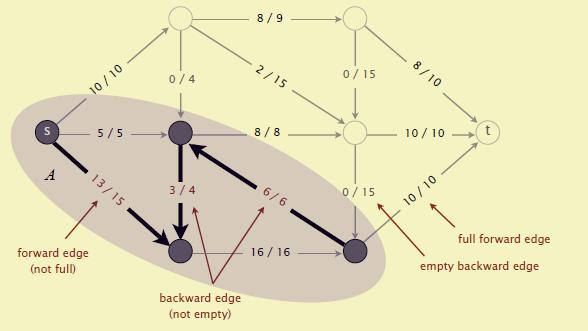
那么根据定义，$s$ 在 $A$ 中，由于没有增广路径，因此 $t$ 在 $B$中。

由于这个割的 $B$ 到 $A$ 的边流量全是 0

这个割的容量 = 沿着这个割的 netflow (从 $A$ 到 $B$ 边的流量 - 从 $B$ 到 $A$ 边的流量)

又根据 flow-value 引理，**net flow = value of low,**因此推出 1

最大流的结果转换为最小割 {#最大流的结果转换为最小割}

根据最大流的解得到最小割的解：就是和证明 3->1 中的一样让割 $cut(A,B)$ 满足这么一个条件：$s$ 在 $A$ 中，且 $A$ 中的顶点通过一些无向的边连接而成，这些边要么是不是满的前向边要么是非空的反向边

把流量已经占满的所有边去掉

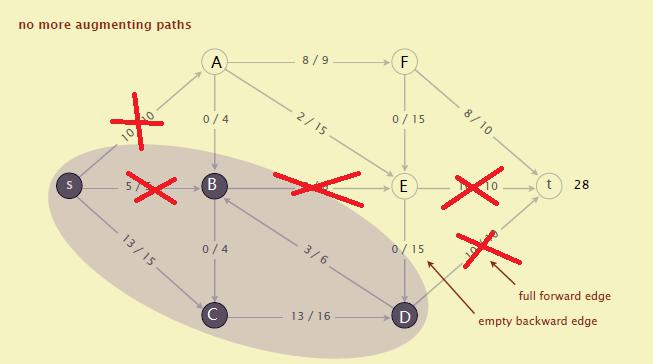
以顶点 $s$ 为起点进行图遍历（遍历的方法可以选择BFS广度优先遍历）。遍历结束后，可以得到遍历经过的所有点：$S、B、C、D$。
把 $S、B、C、D$ 构成一个子图（上图中紫色部分），其他的点 $A、E、F、t$ 构成另一个子图（图中黄色部分）。连接两个子图的边有两种情况：
- 已被占满的前向边：$s$ -> $A$，$B$ -> $E$， $D$ -> $t$
- 没有流量的反向边：$A$ -> $B$， $E$ -> $D$
其中"已被占满的前向边"就是我们要求的最小割。对于上图来说，就是"$s$ -> $A$"、"$B$ -> $E$"、"$D$ -> $t$"这3条边。