当前位置：工具盒子 > Python笔记 > 正文

Python SciPy 实现最小二乘法

2024-11-22 分类：Python笔记阅读(1) 评论(0)

最小二乘法则是一种统计学习优化技术，它的目标是最小化误差平方之和来作为目标，从而找到最优模型。

简介 {#简介}

最小二乘法则是一种统计学习优化技术，它的目标是最小化误差平方之和来作为目标 $J(θ)$，从而找到最优模型的方法，该误差目标定义为： $$ J(\theta)=\min \sum_{i=1}^{m}\left(f\left(x_{i}\right)-y_{i}\right)^{2} $$

Scipy 对优化最小二乘 Loss 的方法做了一些封装，主要有 scipy.linalg.lstsq 和 scipy.optimize.leastsq 两种，此外还有 scipy.optimize.curve_fit 也可以用于拟合最小二乘参数。

scipy.linalg.lstsq {#scipy-linalg-lstsq}

官方文档

SciPy 的 linalg 下的 lstsq 着重解决传统、标准的最小二乘拟合问题，该方法限制了模型 $f(x_i)$的形式必须为 $ f\left(x_{i}\right)=a_{0}+a_{1} x^{1}+a_{2} x^{2}+\cdots+a^{n} x^{n} $ ，对于此类型的模型，给定模型和足够多的观测值 $ y_{i} $ 即可进行求解。

求解时需要将模型 $f(x_i)$ 改写成矩阵形式，矩阵用字母 $A $ 表示，则只需给出方程 $ f\left(x_{i}\right) $ 的模型即 $A$ 及样本 $ y_{i} $ 便可求得方程的各个系数。
函数调用方法：

使用示例 {#使用示例}

例一 {#例一}

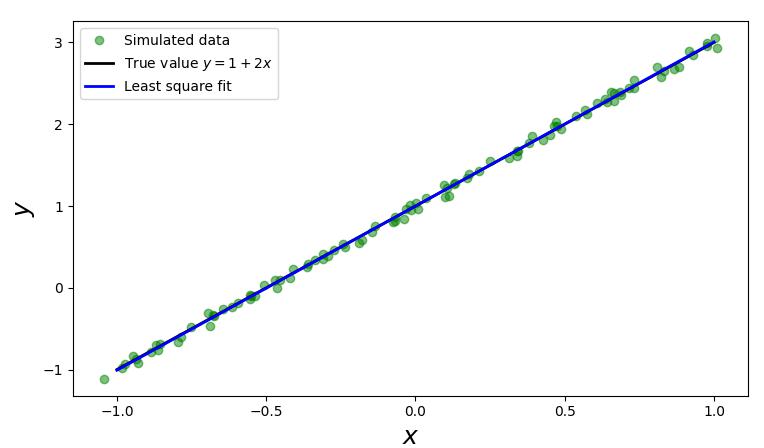
假设真实的模型是 $y=2x+1$，我们有一组数据 $(x_i,y_i)$ 共 100 个，看能否基于这 100 个数据找出 $x_i$
和 $ y_{i} $ 的线性关系方程 $ y=2 x+1 $ ，我们可以通过以下几步来完成。

序构造出100个 $(x_i,y_i)$ 数据。

给出模型 $ f(x)=a+b x $ 的矩阵A。由于有100个观测 $ \left(x_{i}, y_{i}\right) $ 的数据，那么就有:

$$ \begin{aligned} a+b x_{0} & =y_{0} \\ a+b x_{1} & =y_{1} \\ a+b x_{2} & =y_{2} \\ \cdots & \\ a+b x_{99} & =y_{99}\end{aligned} $$

将以上式子写成如下矩阵的形式： $$ \left|\begin{array}{cc}1 & x_{0} \\ 1 & x_{1} \\ \vdots & \vdots \\ 1 & x_{99}\end{array}\right| \times\left|\begin{array}{l}a \\ b\end{array}\right|=\left|\begin{array}{c}y_{0} \\ y_{1} \\ \vdots \\ y_{99}\end{array}\right| $$

调用 scipy.linalg.lstsq 传入 $ A^{T} $ 和观测值里的 $ y_{i} $ 即程序里的yi变量即可求得 $ f(x)=a+b x $ 里的 $a$ 和 $b$。$a$ 和 $b$ 记录在 $Istsq$ 函数的第一个返回值里。

scipy.linalg.Istsq 的第一个返回值 sol 共有两个值， sol[0] 即是估计出来的 $ f(x)=a+b x $ 里的 $a$， $ \operatorname{sol}[1] $ 代表 $ f(x)=a+b x $ 里的 $b$。因此 $ f(x) $ 为:

示例代码

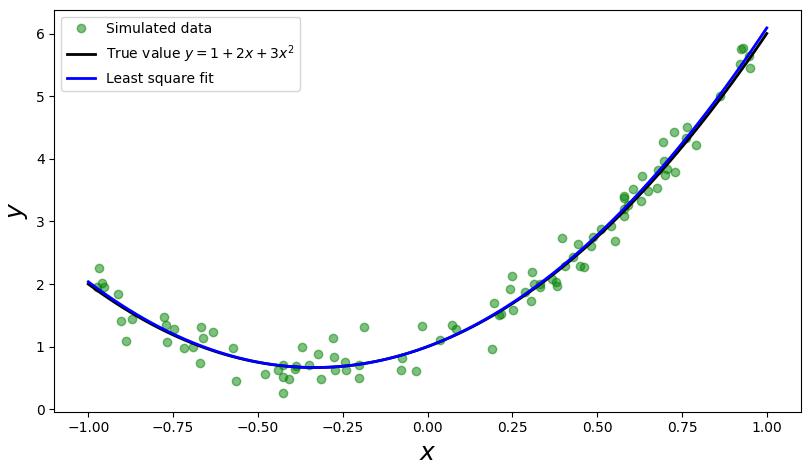
例二 {#例二}

考虑模型为 $f\left(x_{i}\right)=a+b x+c x^{2} $ 的情况：

示例代码

scipy.optimize.leastsq {#scipy-optimize-leastsq}

官方文档

scipy.optimize.leastsq 方法相比于 scipy.linalg.lstsq 更加灵活，开放了 $f(x_i)$ 的模型形式。

leastsq() 函数传入误差计算函数和初始值，该初始值将作为误差计算函数的第一个参数传入。计算的结果是一个包含两个元素的元组，第一个元素是一个数组，表示拟合后的参数；第二个元素如果等于1、2、3、4中的其中一个整数，则拟合成功，否则将会返回 mesg。

调用示例 {#调用示例}

例一 {#例一-2}

首先仍以线性拟合为例，拟合 $ f(x)=a x+b $ 函数。

示例代码

例二 {#例二-2}

这里我们展现一下 leastsq 的灵活之处，由于 leastsq 放开了对 $f(x_i)$ 形式的严格限制，我们可以设置一些更加复杂的最小二乘的情况。

例如我现在就要拟合这么个函数：
$$
f(x)=7e^x+3\frac{1}{\sqrt{x}}+12\sin x
$$
相比于之前的多项式函数可以说有些丧心病狂了，但是也是在 leastsq 射程范围内：

核心函数：

其中: err 为用于计算残差的 Callback 函数，p0 为初始解， args 为输入的数据。

输出结果：

优化方法不是万能的，如果矩阵过于奇异，也是不利于准确求解模型参数的。

scipy.optimize.curve_fit {#scipy-optimize-curve-fit}

官方文档

scipy.optimize.curve_fit 函数用于拟合曲线，给出模型和数据就可以拟合，相比于 leastsq 来说使用起来方便的地方在于不需要输入初始值。

其中 fun 为输入参数为 $x$ 和模型参数列表，输出 $y$ 的 Callback 函数，$X$ 和 $Y$ 为数据

调用示例 {#调用示例-2}

例一 {#例一-3}

为了方便对比，将上文例二的示例代码修改成 curve_fit 函数的实现

示例代码：

输出结果：

绘制图像：

效果没有 leastsq 稳定，可能是没有初始值的缘故。

参考资料 {#参考资料}

文章链接：
https://www.zywvvd.com/notes/coding/python/scipy-leastsquare/scipy-leastsquare/

未经允许不得转载：工具盒子 » Python SciPy 实现最小二乘法

标签： scipy 最小二乘法

厉飞雨

众生皆苦，唯有自渡！

相关推荐