EXERCISE 4.3. A validation problem.
A rectangular plate is loaded on one edge and supported on the opposite edge as shown. Assuming that these supports and loads are evenly distributed along the edges to which they are applied, and that the plate behaves as a plane stress structure, compute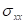 ,
, 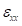 , and the corner (nodal) displacements. Use mechanics, not the finite element approximations, to compute the required quantities.
, and the corner (nodal) displacements. Use mechanics, not the finite element approximations, to compute the required quantities.
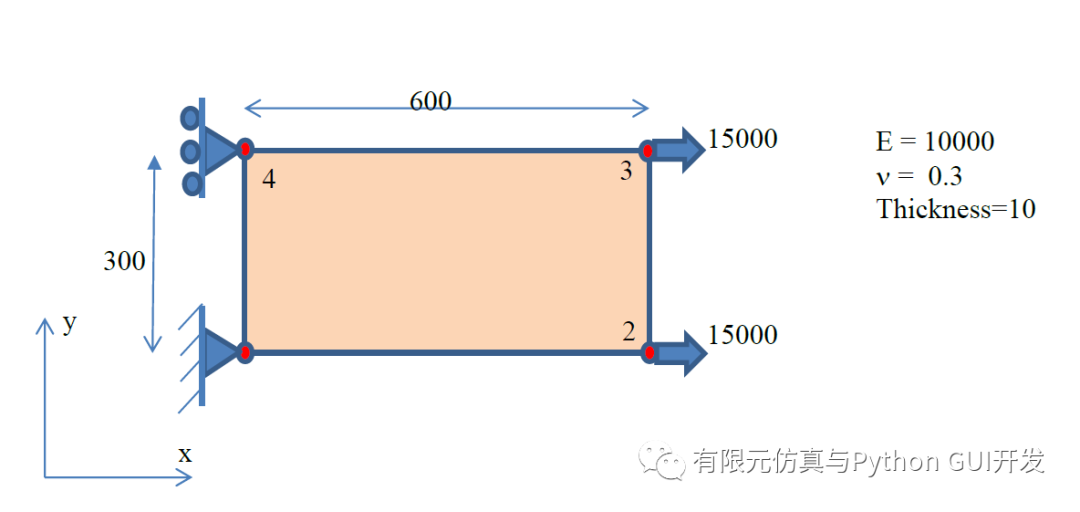
Solution:
This problem is a plane stress problem where E=10000 and v=0.3, so the D matrix is:
|---------------------------------------------------------------------------------------------------------------------------|
| 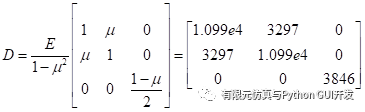 |
|
For a quadrilateral four-node element, there are four Gaussian integral points, which are ( -1/sqrt(3), -1/sqrt(3) ), ( -1/sqrt(3), 1/sqrt(3) ),
( 1/sqrt(3), -1/sqrt(3) ), ( 1/sqrt(3), 1/sqrt(3) ).
1.Gaussian integral points ( -1/sqrt(3), -1/sqrt(3) )
the shape function at ( -1/sqrt(3), -1/sqrt(3) ) is
|---------------------------------------------------------------------------------------------------------------------------|
|  |
|
The local derivatives at ( -1/sqrt(3), -1/sqrt(3) ) is:
|---------------------------------------------------------------------------------------------------------------------------|
| 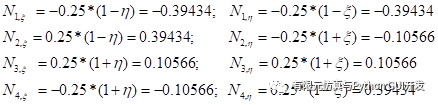 |
|
The Jacobian matrix:
|---------------------------------------------------------------------------------------------------------------------------|
| 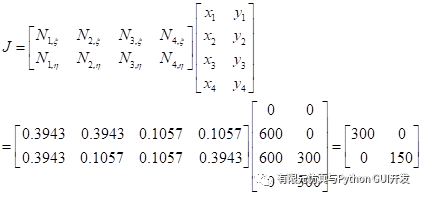 |
|
The determinant of the Jacobian matrix is det(J)=45000
the B matrix is
|-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 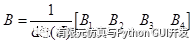
 |
|
Where
|---------------------------------------------------------------------------------------------------------------------------|
| 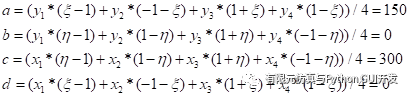 |
|
So that:
|-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 
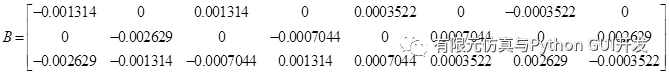 |
|
The stiffness matrix at the Gaussian integral point ( -1/sqrt(3), -1/sqrt(3) ) is
|---------------------------------------------------------------------------------------------------------------------------|---------------------------------------------------------------------------------------------------------------------------|
| 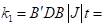 |
| 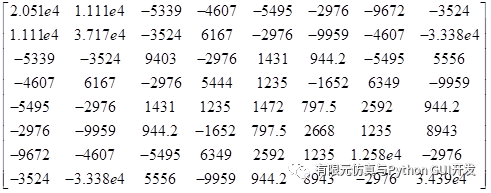 |
|
2.Gaussian integral points ( 1/sqrt(3), -1/sqrt(3) )
The stiffness matrix at the Gaussian integral point ( 1/sqrt(3), -1/sqrt(3) ) is
|---------------------------------------------------------------------------------------------------------------------------|---------------------------------------------------------------------------------------------------------------------------|
| 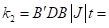 |
| 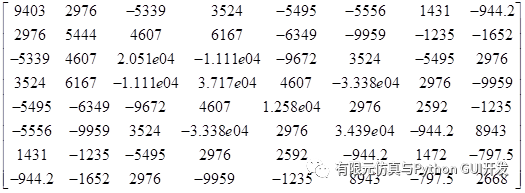 |
|
3.Gaussian integral points ( 1/sqrt(3), 1/sqrt(3) )
The stiffness matrix at the Gaussian integral point ( 1/sqrt(3), 1/sqrt(3) ) is
|---------------------------------------------------------------------------------------------------------------------------|---------------------------------------------------------------------------------------------------------------------------|
| 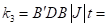 |
| 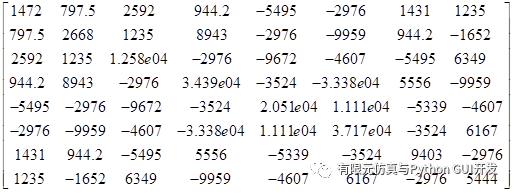 |
|
4.Gaussian integral points ( -1/sqrt(3), 1/sqrt(3) )
The stiffness matrix at the Gaussian integral point ( -1/sqrt(3), 1/sqrt(3) ) is
|---------------------------------------------------------------------------------------------------------------------------|---------------------------------------------------------------------------------------------------------------------------|
| 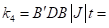 |
| 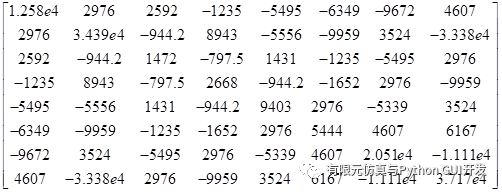 |
|
The element stiffness matrix of quadrilateral four-node is:
|---------------------------------------------------------------------------------------------------------------------------|
| 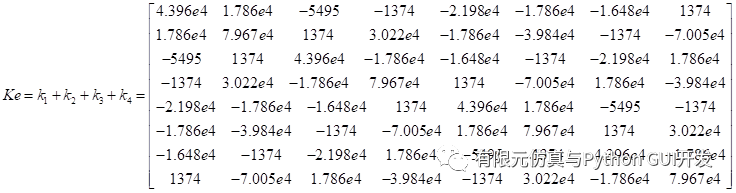 |
|
The node load vector is
|---------------------------------------------------------------------------------------------------------------------------|
|  |
|
The node displacement is
|---------------------------------------------------------------------------------------------------------------------------|
|  |
|
Using the method of removing rows and columns to solve the equilibrium equation:
|-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 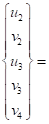
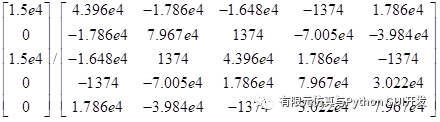
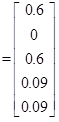
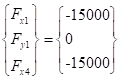 |
|
Calculate the stress at ( -1/sqrt(3), 1/sqrt(3) ):
|---------------------------------------------------------------------------------------------------------------------------|
| 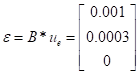 |
|
Compute stresses:
|---------------------------------------------------------------------------------------------------------------------------|
|  |
|
 51工具盒子
51工具盒子