51工具盒子对于多人完成多个代价不同的任务的指派问题，匈牙利算法是一种有效的解决方案，本文记录相关内容。
指派问题 {#指派问题}
- 在生活中经常遇到这样的问题，某单位需完成$n$项任务，恰好有$n$个人可承担这些任务。由于每人的专长不同，各人完成任务的代价不同（收益不同）。于是产生应指派哪个人去完成哪项任务，使完成$n$项任务的总代价最小（收益最大）。这类问题称为指派问题或分派问题。
- 这类问题可以依据人员和代价（收益）建立矩阵，称为效率矩阵或系数矩阵，其元素 $𝑐_{𝑖𝑗}＞0(𝑖,𝑗 = 1,2,...,𝑛)$表示指 派第𝑖人去完成第𝑗项任务时的效率(或时间、成本等)。
- 代价矩阵有一个性质，若从指派问题的系数矩阵的某行（列）各元素中分别减去或者加上常数$k$，其最优任务分解问题不变。
匈牙利算法 {#匈牙利算法}
叫做
匈牙利算法的事实上有两个算法，分别解决指派问题和二分图最大匹配求解问题，此处算法指求解指派问题的匈牙利算法。
算法流程 {#算法流程}
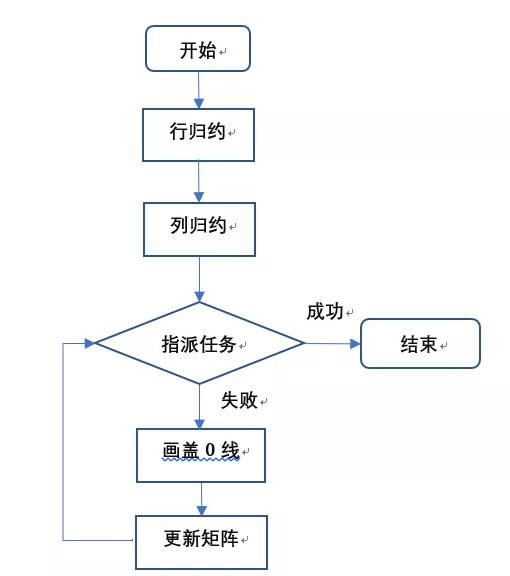
算法内容 {#算法内容}
第一步 {#第一步}
-
数矩阵经变换，在各行各列中都出现0 元素。
- 使指派问题的系数矩阵经变换，在各行各列中都出现0 元素。
- 从系数矩阵的每行元素减去该行的最小元素；
- 从所得系数矩阵的每列元素中减去该列的最小元素。
- 若某行(列)已有0元素，那就不必再减了。
每行每列最小元素非负
第二步 {#第二步}
进行试指派，以寻求最优解。为此，按以下步骤进行。
- 经第一步变换后，系数矩阵中每行每列都已有了0元素；但需找出𝑛个独立的0元素。若能找出，就以这些独立0元素对应解矩阵 $(𝑥_{𝑖,𝑗})$中的元素为1，其余为0，这就得到最优解。
- 步骤为：
- 从只有一个0元素的行(列)开始，给这个0元素加圈，记作◎ 。这表示对这行所代表的人，只有一种任务可指派。然后划去◎ 所在列(行)的其他0元素，记作Φ。这表示这列所代表的任务已指派完，不必再考虑别人了。
- 只有一个0元素列(行)的0元素加圈，记作◎；然后划去◎ 所在行的0元素，记作Φ。
- 反复进行(1)，(2)两步，直到所有0元素都被圈出和划掉为止。
- 若仍有没有划圈的0元素，且同行(列)的0元素至少有两个( 表示对这个可以从两项任务中指派其一)。这可用不同的方案去试探。从剩有0元素最少的行(列)开始，比较这行各0元素所在列中0元 素的数目，选择0元素少的那列的这个0元素加圈 (表示选择性多的要"礼让"选择性少的)。然后划掉同行同列的其他0元素。可反复进行，直到所有0元素都已圈出和划掉为止。
- 若◎元素的数目𝑚等于矩阵的阶数𝑛，那么这指派问题的最优解已得到。若𝑚＜𝑛，则转入下一步。
第三步 {#第三步}
- (𝑚 < 𝑛时的处理办法)：作最少的直线覆盖所有0元素，以确定该系数矩阵中能找到最多的独立元素数。
- 为此按以下步骤进 行：
- 对没有◎的行打√号；
- 对已打√号的行中所有含◎元素的列打√号；
- 再对打有√号的列中含◎元素的行打√号；
- 重复(2)，(3)直到得不出新的打√号的行、列为止。
- 对没有打√号的行画一横线，有打√号的列画一纵线，这就得到覆盖所有0元素的最少直线数。
令这直线数为𝑙。若𝑙＜𝑛，说明必须再变换当前的系数矩阵，才能找到𝑛个独立的0元素，为此需要转第四步：若l=n，而m＜n， 应回到第二步(4)，另行试探。
第四步 {#第四步}
- 对矩阵进行变换的目的是增加0元素。
- 为此，在没有被直线覆盖的部分中找出最小元素，然后在打√行各元素中都减去这最小元素，而在打√列的各元素都加上这最小元素，以保证原来0元素不变。
- 这样得到新系数矩阵(它的最优解和原问题相同)。若得到𝑛个独立的0元素，则已得最优解，否则回到第三步重复进行。
算法示例 {#算法示例}
有$A、B、C、D、 E$五项任务，需要分配给$甲、乙、丙、丁、戊$ 五个人来完成。他们完成任务所需要支付的酬劳如下表所示，问，如何分配任务，可使总费用最少？
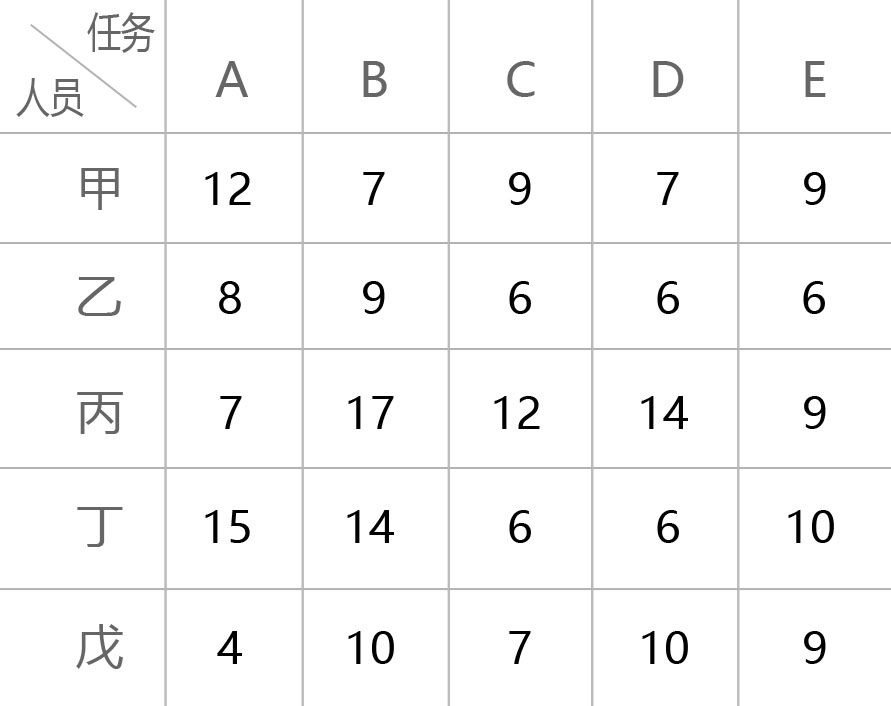
一、减法归约 {#一、减法归约}
-
行归约：每行元素减去该行最小元素。
-
画圈为行最小值：
-
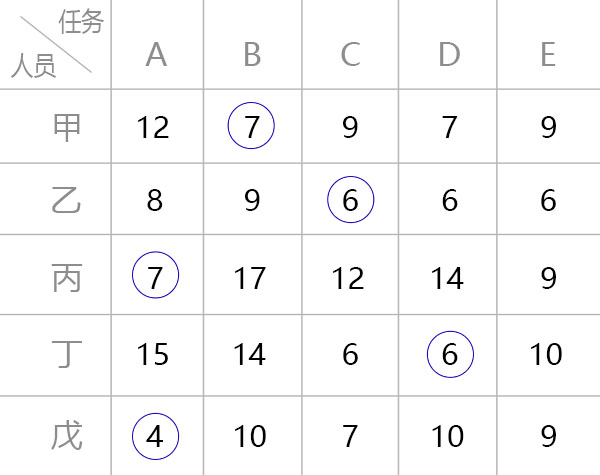
每行减去最小值：
-
-
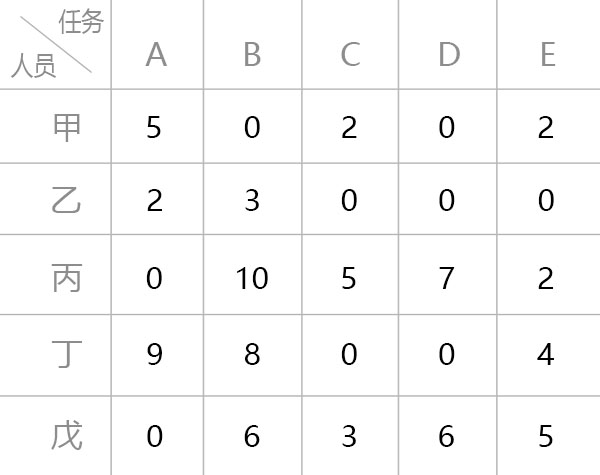
列归约：每行元素减去该行最小元素。
- 每列最小值已经为 0 无须继续归约：
二、圈零划零 {#二、圈零划零}
- 找到含零元素最少的行，对零元素打圈，划去打圈零元素所在行和列存在的零元素，重复这个步骤，直到矩阵中所有的零元素都被处理完。
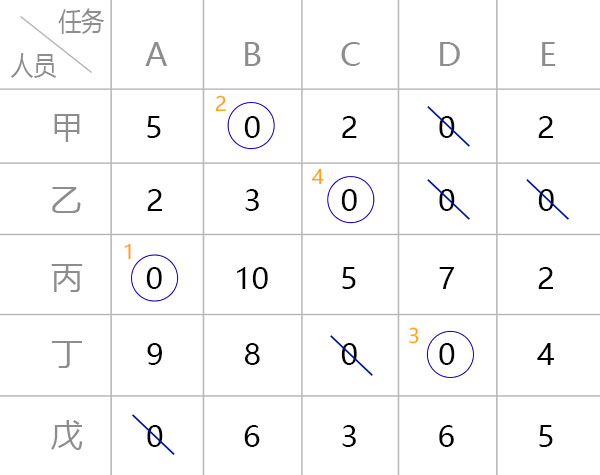
三、打勾划线 {#三、打勾划线}
- 打钩
- 无
〇行打钩√ - 无
〇行有〇列打钩√ √列有〇行打钩√
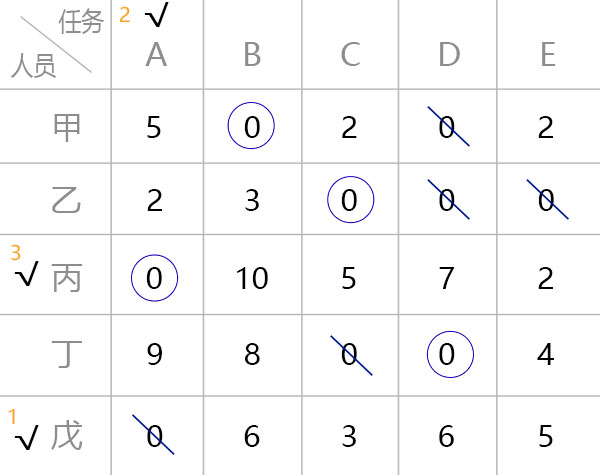
- 划线
- 无
√行划线 - 有
√列划线
得到覆盖所有0元素的最少直线数。
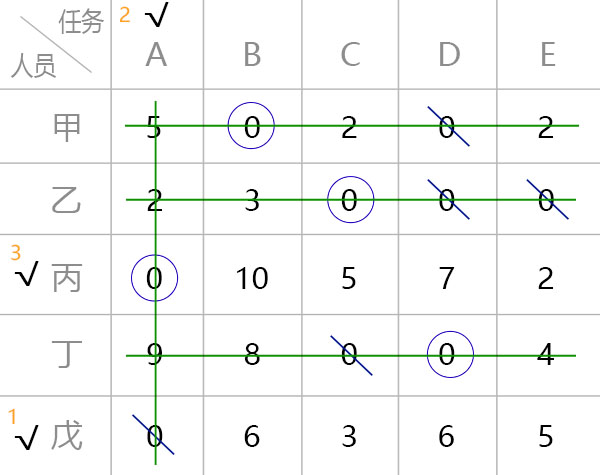
- 此时线数为4，少于节点数5，需要进入下一个调整值的步骤
四、元素调整 {#四、元素调整}
- 在没有被直线覆盖的部分选择最小值，作为调整元素
-
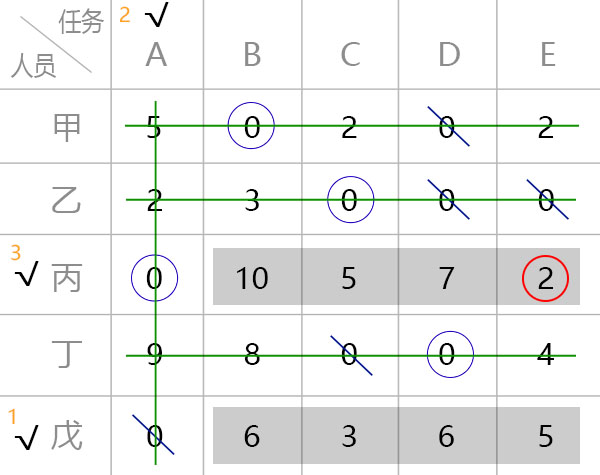
划线列，不划线行为需要调整的行列 （划
√的行列） -
调整行减去调整元素
-
调整列加上调整元素
此种操作会保证行中的 0 元素不变
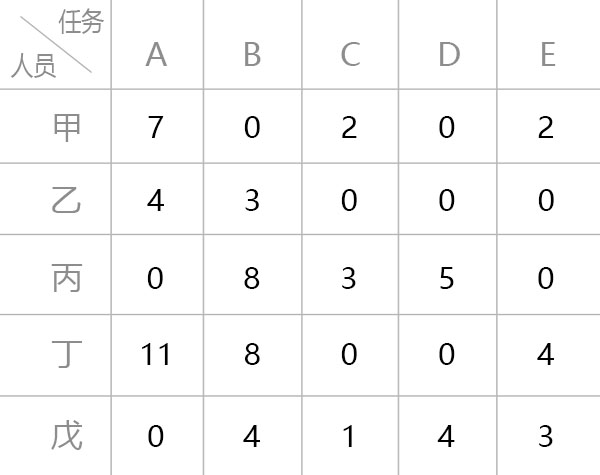
五、重新圈零 {#五、重新圈零}
-
重新进行第三步圈零操作
乙和丁的任务可以交换
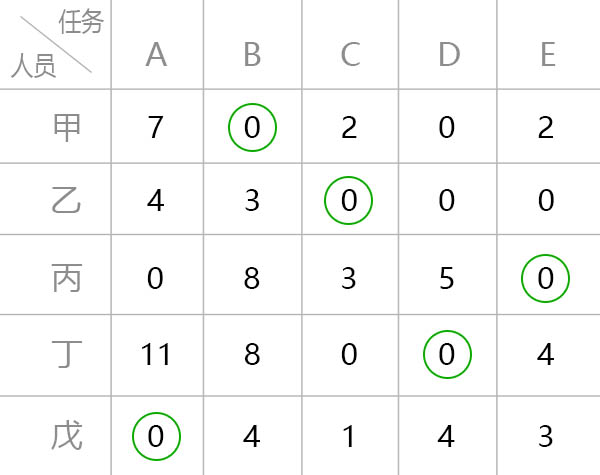
- 因此指派方案确定
| | 甲 | 乙 | 丙 | 丁 | 戊 | |------|---|---|---|---|---| | 任务安排 | B | C | E | D | A |
- 最终匈牙利算法的结果
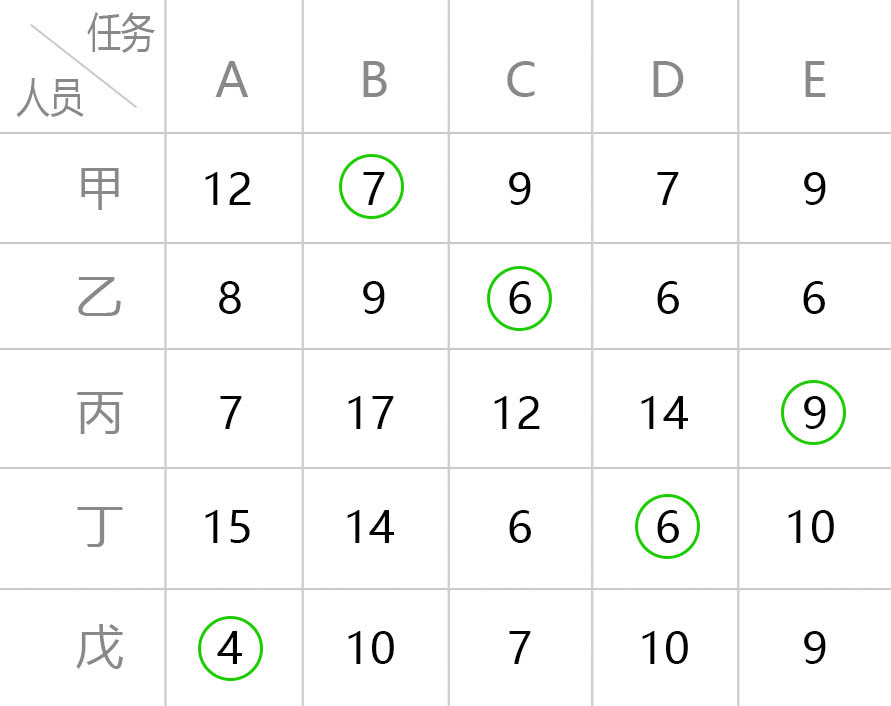
- 总共花费的费用和为 32
Python 实现 {#Python-实现}
- python 解决方案中，用到的是
scipy.optimize.linear_sum_assignment(cost_matrix) - 以上文的算法示例为例
- 输出结果
参考资料 {#参考资料}
- https://www.cnblogs.com/ylHe/p/9287384.html
- https://www.pianshen.com/article/35751358181/
- https://www.freesion.com/article/5336622238/
- https://blog.csdn.net/qq_40894102/article/details/105980364
- https://blog.csdn.net/siss0siss/article/details/51325656
文章链接：
https://www.zywvvd.com/notes/study/math/hubgairan-assignment/hubgairan-assignment/
