图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图,匈牙利算法是求解二分图最大匹配的一种方法,本文介绍相关内容。
定义 {#定义}
二分图 {#二分图}
图中的边均为无向无权边
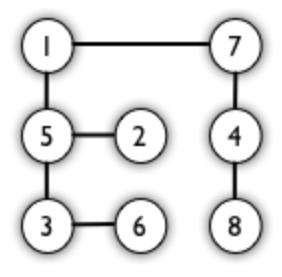
- 简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。
- 准确地说:把一个图的顶点划分为两个不相交集$U$和$V$,使得每一条边都分别连接$U$、$V$中的顶点。如果存在这样的划分,则此图为一个二分图。
- 二分图的一个等价定义是:不含有「含奇数条边的环」的图。
图 1 是一个二分图。为了清晰,把它画成图 2 的形式。
|-------------------------------------------------------------------------------------------------------------------------------|-------------------------------------------------------------------------------------------------------------------------------|
|  |
|  |
| 图1 | 图2 |
|
| 图1 | 图2 |
匹配 {#匹配}
在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。
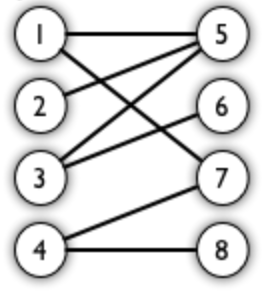
例如,图 3、图 4 中红色的边就是图 2 的匹配。
匹配点 、匹配边 、未匹配点 、非匹配边 {#匹配点、匹配边、未匹配点、非匹配边}
它们的含义非常显然。
例如图 3 中 1、4、5、7 为匹配点,其他顶点为未匹配点;1-5、4-7为匹配边,其他边为非匹配边。
|-------------------------------------------------------------------------------------------------------------------------------|-------------------------------------------------------------------------------------------------------------------------------|
|  |
|  |
| 图3 | 图4 |
|
| 图3 | 图4 |
最大匹配 {#最大匹配}
一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。
图 4 是一个最大匹配,它包含 4 条匹配边。
完美匹配 {#完美匹配}
如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。
图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
最大匹配数 {#最大匹配数}
最大匹配的匹配边的数目
最小点覆盖数 {#最小点覆盖数}
选取最少的点,使任意一条边至少有一个端点被选择
最小路径覆盖数 {#最小路径覆盖数}
对于一个 DAG(有向无环图),选取最少条路径,使得每个顶点属于且仅属于一条路径。路径长可以为 0(即单个点)。
最大独立数 {#最大独立数}
选取最多的点,使任意所选两点均不相连
定理 {#定理}
- 最大匹配数 = 最小点覆盖数(Konig 定理)
- 最大匹配数 = 最大独立数
- 最小路径覆盖数 = 顶点数 - 最大匹配数
匈牙利算法 {#匈牙利算法}
叫做
匈牙利算法的事实上有两个算法,分别解决指派问题和二分图最大匹配求解问题,此处算法指求解二分图最大匹配的匈牙利算法。
增广路 {#增广路}
从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。
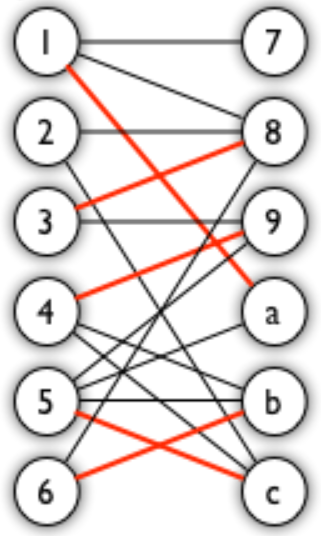
例如,图 5 中的一条增广路如图 6 所示(图中的匹配点均用红色标出):
|-------------------------------------------------------------------------------------------------------------------------------|-------------------------------------------------------------------------------------------------------------------------------|
|  |
|  |
| 图5 | 图6 |
|
| 图5 | 图6 |
- 增广路有一个重要特点:非匹配边比匹配边多一条。因此,研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边,所以这样做不会破坏匹配的性质。交换后,图中的匹配边数目比原来多了 1 条。
匈牙利树 {#匈牙利树}
一般由 BFS 构造(类似于 BFS 树)。从一个未匹配点出发运行 BFS(唯一的限制是,必须走交替路),直到不能再扩展为止。
例如,由图 7,可以得到如图 8 的一棵 BFS 树:
|-------------------------------------------------------------------------------------------------------------------------------|-------------------------------------------------------------------------------------------------------------------------------|
|  |
|  |
| 图7 | 图8 |
|
| 图7 | 图8 |
这棵树(图8)存在一个叶子节点为非匹配点(7 号),但是匈牙利树要求所有叶子节点均为匹配点,因此这不是一棵匈牙利树;
但图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路,沿这条增广路扩充后将得到一个完美匹配;
真正的匈牙利树如下图所示:

算法思路 {#算法思路}
- 可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时,达到最大匹配(这是增广路定理)。
匈牙利算法 {#匈牙利算法-2}
- 从左边第 1 个顶点开始,挑选未匹配点进行搜索,寻找增广路。
- 如果经过一个未匹配点,说明寻找成功。更新路径信息,匹配边数 +1,停止搜索。
- 如果一直没有找到增广路,则不再从这个点开始搜索。事实上,此时搜索后会形成一棵匈牙利树。我们可以永久性地把它从图中删去,而不影响结果。
- 由于找到增广路之后需要沿着路径更新匹配,所以我们需要一个结构来记录路径上的点。DFS 版本通过函数调用隐式地使用一个栈,而 BFS 版本使用
prev数组。
算法示例 {#算法示例}
- 以男生女生结成情侣的场景为例,有男生节点和女生节点组成的二分图,部分男生女生之间互有好感,那么最多可以组成多少对情侣
- 数学表述: 求解二分图中最多能找到多少条没有公共端点的边 / 二分图的最大匹配数

算法流程 {#算法流程}
- 从B1看起,他对G2有好感,暂时把他与G2连接(注意这时只是你作为一个红娘在纸上构想,没有真正行动)。

- 接下来看 B2,B2也喜欢G2,这时G2已经"名花有主"了(虽然只是我们设想的),那怎么办呢?我们倒回去看G2目前被安排的男友,是B1,B1有没有别的选项呢?有,G4,G4还没有被安排,那我们就给B1安排上G4。

- 然后B3,B3直接配上G1就好了,这没什么问题。至于B4,他只钟情于G4,G4目前配的是B1。B1除了G4还可以选G2,但是呢,如果B1选了G2,G2的原配B2就没得选了。我们绕了一大圈,发现B4只能注定单身了,可怜。

算法复杂度 {#算法复杂度}
- 以上就是匈牙利算法的基本流程,时间复杂度为 $O(n^3)$
- 需要找$O(n)$次增广路
- 对每个节点搜索增广路径时,边数上限为$n^2$,因此复杂度为 $O(n^2)$
最小点覆盖问题 {#最小点覆盖问题}
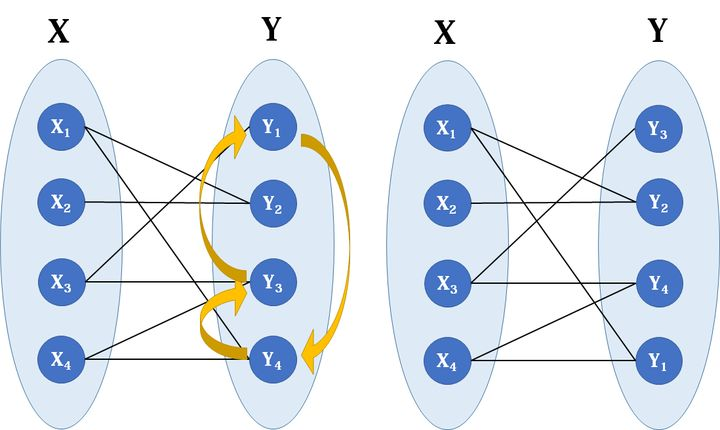
另外一个关于二分图的问题是求最小点覆盖 :我们想找到最少 的一些点 ,使二分图所有的边都至少有一个端点在这些点之中。倒过来说就是,删除包含这些点的边,可以删掉所有边。
- 根据 König 定理:一个二分图中的最大匹配数等于这个图中的最小点覆盖数;
- 因此该问题可以用上述匈牙利算法解决;
- 从左侧一个未匹配成功的点 出发,走一趟匈牙利算法的流程(即紫色的箭头),所有左侧未经过的点 ,和右侧经过的点,即组成最小点覆盖。

匈牙利算法的应用 {#匈牙利算法的应用}
匈牙利算法可以用来解决一些看似无关的问题。
矩阵游戏 {#矩阵游戏}
题目描述
小Q是一个非常聪明的孩子,除了国际象棋,他还很喜欢玩一个电脑益智游戏――矩阵游戏。矩阵游戏在一个$N×N$ 黑白方阵进行(如同国际象棋一般,只是颜色是随意的)。每次可以对该矩阵进行两种操作:
行交换操作:选择矩阵的任意两行,交换这两行(即交换对应格子的颜色)
列交换操作:选择矩阵的任意两列,交换这两列(即交换对应格子的颜色)
游戏的目标,即通过若干次操作,使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。
对于某些关卡,小Q百思不得其解,以致他开始怀疑这些关卡是不是根本就是无解的!于是小Q决定写一个程序来判断这些关卡是否有解。
输入格式
第一行包含一个整数T,表示数据的组数。
接下来包含T组数据,每组数据第一行为一个整数N,表示方阵的大小;接下来N行为一个$N×N$ 的01矩阵(0表示白色,1表示黑色)。
输出格式
包含T行。对于每一组数据,如果该关卡有解,输出一行Yes;否则输出一行No。
-
我们把矩阵转化为二分图(左侧集合代表各行,右侧集合代表各列,某位置为1则该行和该列之间有边)。我们想进行一系列交换操作,使得X1连上Y1,X2连上Y2,......
-
大家可以想象,所谓的交换 ,是不是可以等价为重命名?我们可以在保持当前二分图结构不变的情况下,把右侧点的编号进行改变,这与交换的效果是一样的。
-
所以想让X1、X2...与Y1、Y2...一一对应,其实只需要原图最大匹配数为4就行了。
CoVH之柯南开锁 {#CoVH之柯南开锁}
由$M*N$个格子组成, 其中某些格子凸起(灰色的格子)。每一次操作可以把某一行或某一列的格子给按下去。需要在限定次数把所有格子按下去,请计算出开给定的锁所需的最少次数。

读入/Input:
第一行 两个不超过100的正整数N, M表示矩阵的长和宽
以下N行 每行M个数 非0即1 1为凸起方格输出/Output:
一个整数 所需最少次数
- 如果我们把样例的矩阵,转化为二分图的形式,是这样的:

- 按下一行或一列,其实就是删掉与某个点相连的所有边。现在要求最少的操作次数,想想看,这不就是求最小点覆盖数吗?所以直接套匈牙利算法即可。
棋盘覆盖 {#棋盘覆盖}
描述 Description
给出一张nn(n<=100)的国际象棋棋盘,其中被删除了一些点,问可以使用多少1 2的多米诺骨牌进行掩盖。
输入格式 Input Format
第一行为n,m(表示有m个删除的格子)
第二行到m+1行为x,y,分别表示删除格子所在的位置
x为第x行
y为第y列
输出格式 Output Format
一个数,即最大覆盖格数
- 经典的多米诺覆盖问题大家都很熟悉,我们把棋盘染色,每个多米诺骨牌恰好覆盖一个白格和一个黄格。

- 在染色之后,黑格和白格可以构成一个二分图,每个白格都只和黑格相连,每个黑格也只和白格相连。
- 在给所有黑格和白格编号后,我们把每个未删除的格子都与它 上下左右紧邻 的未删除的格子相连。
- 这张二分图的最大匹配数,就是我们能放下最多的多米诺骨牌数。注意因为数据范围较大,要用邻接表存图。
参考资料 {#参考资料}
文章链接:
https://www.zywvvd.com/notes/study/math/hungarian-binary/hungarian-binary/
 51工具盒子
51工具盒子