# (一)场景描述 {#一-场景描述}
在对大量网站进行网页爬虫时,一般需要两步,先对url进行搜集,再对每一个url进行爬取。这里很有可能搜集到的url是重复的,因此需要在第一步对url进行去重。如何去重呢?你会想到将url放进HashSet中,但是如果url的数量过大,HashSet是撑不住的。
我们在看新闻或者看抖音时,它会不停推荐新内容给我们,推荐时需要去除已经看过的内容,那么如何实现去重呢?你会想到服务器记录了用户看过的所有记录,推荐时从历史记录中去筛选,但是当用户量很大,并且用户看过的新闻很多,性能能跟上吗?
另外在遇到缓存穿透问题时,请求绕过缓存直接读取持久层数据库,能否在请求来的时候先进行一次过滤,如果确定所请求的key在数据库不存在时,直接过滤掉?
上面的这些场景,都可以使用布隆过滤器(Bloom Filter)来实现。
# (二)布隆过滤器是什么 {#二-布隆过滤器是什么}
可以把布隆过滤器理解为一个不怎么精确的set结构,它能在实现去重的同时,在空间上节省90%以上,之所以说它是不怎么精确的,因为布隆过滤器在去重时存在误差。
当布隆过滤器说一个值不存在时,它一定不存在;但是当布隆过滤器说一个值存在时,它是有可能不存在的。 理解这个概念十分重要,不能理解反了。重新看一下上面的场景,第一个爬虫场景,将已经爬取的url放入布隆过滤器,当有新的url进来时,先用contains方法判断这个对象是否存在,如果判断是不存在时,那说明一定不存在,如果判断是存在的,即使有可能不存在,但那也是极小的误差,丢了即可。
在新闻推荐的场景也是一样,布隆过滤器可以准确过滤已经看过的内容,虽然会过滤掉(误差)极小数没看过的内容,但是对用户来说没有任何影响。 缓存穿透问题解决方式也一样。
# (三)Redis中使用布隆过滤器 {#三-redis中使用布隆过滤器}
这里都是linux下的操作,bloomFilter的下载和安装简单介绍一下:
wget https://github.com/RedisLabsModules/rebloom/archive/v1.1.1.tar.gz
cp v1.1.1.tar.gz /usr/local/redis-6.0.6
cd /usr/local/redis-6.0.6
tar -zxvf v1.1.1.tar.gz
cd RedisBloom-1.1.1/
make
1
2
3
4
5
6

在redis.conf中加入该模块
################################## MODULES #####################################
loadmodule /usr/local/redis-6.0.6/RedisBloom-1.1.1/rebloom.so
1
2
布隆过滤器有两个基本的指令,bf.add 和 bf.exists。如果想要一次性添加多个元素就可以使用bf.madd 以及使用 bf.mexists查询多个元素是否存在
127.0.0.1:6379> bf.add user 1
(integer) 1
127.0.0.1:6379> bf.exists user 1
(integer) 1
127.0.0.1:6379> bf.exists user 2
(integer) 0
127.0.0.1:6379> bf.madd user 2,3,4
1) (integer) 1
127.0.0.1:6379> bf.mexists user 2,3,4
1) (integer) 1
127.0.0.1:6379> bf.mexists user 2,3,4,5
1) (integer) 0
1
2
3
4
5
6
7
8
9
10
11
12
看上去确实很精确啊,不要急,我们加大力度。接下使用java对一万个数据进行误判检测。 首先引入jar包:
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>22.0</version>
</dependency>
1
2
3
4
5
通过代码分别选取10000个存在于布隆过滤器中的元素和10000不存在于布隆过滤器中的元素进行误判检测:
public class Test {
public static void main(String[] args) {
//创建布隆过滤器,并放进去10000个元素
BloomFilter<Integer> bloomFilter=BloomFilter.create(Funnels.integerFunnel(),10000);
for (int i = 0; i < 10000; i++) {
bloomFilter.put(i);
}
System.out.println("======================数据导入成功==========================");
int count=0;
//选取10000个存在于布隆过滤器中的元素,查询误判的数量
for (int i=0;i<10000;i++){
if (!bloomFilter.mightContain(i)){
count++;
}
}
System.out.println("======================查询存在于布隆过滤器中的元素,误判的次数为:"+count+"===============");
count=0;
//选取10000个不存在于布隆过滤器中的元素,查询误判的数量
for (int i = 10000; i < 20000; i++) {
if (bloomFilter.mightContain(i)){
count++;
}
}
System.out.println("======================查询不存在于布隆过滤器中的元素,误判的次数为:"+count+"===============");
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
最终的结果如下:
======================数据导入成功==========================
======================查询存在于布隆过滤器中的元素,误判的次数为:0===============
======================查询不存在于布隆过滤器中的元素,误判的次数为:318===============
1
2
3
可以看到,对于布隆过滤器中已有的元素,是不会存在误判的,对不存在于布隆过滤器中的元素,查询出误判率大约为0.03。这个误判率可由自己设置

我们修改一下上面的代码,在创建布隆过滤器时传入一个可接受的误差值:
BloomFilter<Integer> bloomFilter=BloomFilter.create(Funnels.integerFunnel(),10000,0.01);
1
再次运行代码,查看结果:
======================数据导入成功==========================
======================查询存在于布隆过滤器中的元素,误判的次数为:0===============
======================查询不存在于布隆过滤器中的元素,误判的次数为:94===============
1
2
3
但是减少误差是以空间换取准确率,在实际的使用中,需要根据需求来修改这个误差值。比如新闻去重上,误判率高一些只会让小部分文章不能让合适的人看到,但是却能节省较大的空间。
# (四)布隆过滤器的原理 {#四-布隆过滤器的原理}
原理这东西只需要你能在脑海中想象到布隆过滤器执行的过程,对于其中的计算涉及到高等数学、离散数学等知识,我们就不需要去深究了。
每个布隆过滤器对应于一个大型的位数组和几个不一样的无偏hash函数,所谓无偏hash函数就是能把元素的hash值计算较为均匀。
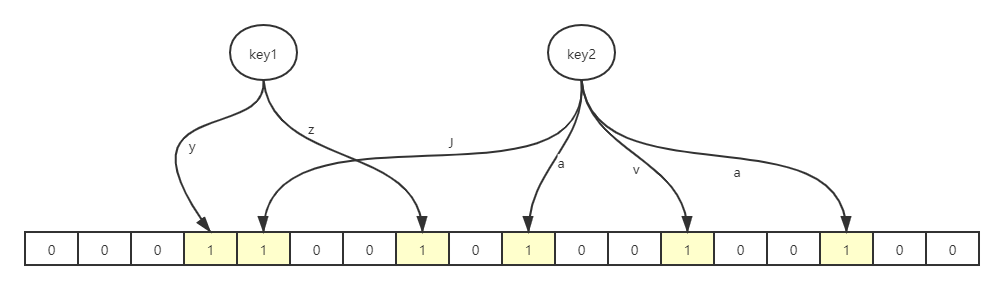
以add添加key的操作为例,首先会使用多个hash函数计算key的整数索引,再把对应的数组的这几个位置置为1,这样就完成了add操作。
向布隆过滤器询问这个key是否存在时,也一样先计算出一个hash值,再看看这几个位置是否都为1,只要有一个为0,就说明这个key不存在。但是如果都是1,却不一定说明这个key一定存在,因为这些位被置为1可能是因为其他的key所导致的。
因此布隆过滤器的特性已经可以很好的解释了,如果我们将这个位数组变得大一些,冲突的几率就会降低,误差自然也就降低,同理如果设置的位数组小,误差的概率就大了,以空间换精度。
在使用过程中,我们需要提前预估元素的数量,如果实际的元素超出预估数量,预判率将会大幅上升。
# (五)总结 {#五-总结}
布隆过滤器的应用比较简单,但是内部的原理涉及到极为复杂的数学知识,关于原理我建议大家只需要知道运行原理即可。对于使用,希望大家能亲手操作一番。
 51工具盒子
51工具盒子