一、二叉树、B树、B+树及其特点
二叉树
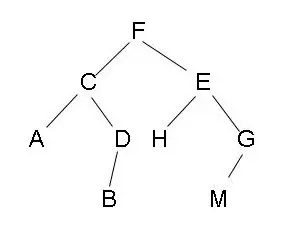
特点:
-
所有非叶子结点至多拥有两个儿子(Left和Right);
-
每个结点各存储一个关键字;
-
非叶子结点的左指针指向小于其关键字的子树,右指针指向大于其关键字的子树;
B树
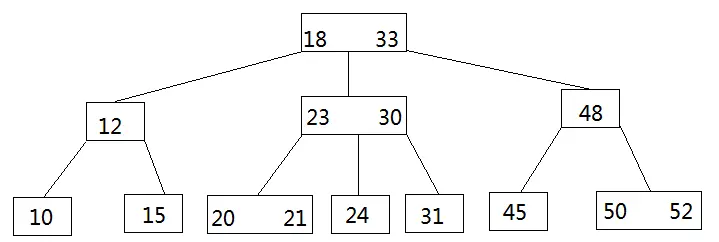
特点:
-
B树中每个节点可以有多个关键字,并且每个节点可以有多个孩子;
-
B树中同一键值不会出现多次,要么在叶子节点上,要么在内结点上;
-
由于B树的每个结点都存真实的数据,会导致每一个结点存储的数据量变小,整个B树的层数就会相对变高,数据量变大之后,最终会变成一个瘦高个子,导致搜索或修改的性能就会越低。
-
查找效率与键在B树中的位置有关,在叶子结点的时候,最大时间复杂度为O(log n),在根结点的时候,最小时间复杂度为O(1);
-
B树中所有节点的孩子节点数中的最大值称为B树的阶,记为M
-
树中的每个节点至多有M棵子树
-
若根节点不是终端节点,则至少有两棵子树
-
除根节点外所有非叶节点至少有m/2棵子树
-
所有的叶节点需要出现在同一层次上
-
树中所有节点的平衡因子都等于0
B+树
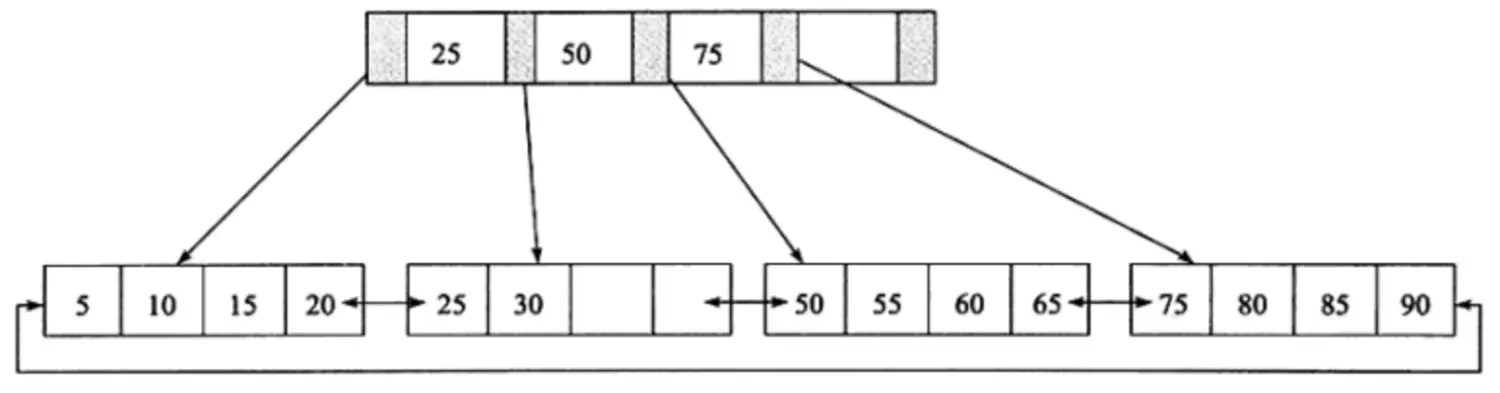
特点:
-
B+树的键一定会出现在叶子结点上,同时也可能在非叶子结点中重复出现。简单说,B+树的内结点存储的都是键值,键值对应的具体数据都存储在叶子结点上;
-
B+树的内结点只存键值,故存储的记录比B树内结点多很多,故B+树是横向扩展的,最终会长成一个矮胖子,在搜索时,最终只需要从根到叶子结点遍历层数(比B树这个高瘦子的层数少很多)个结点即可,性能会比较高。
-
B+树的时间复杂度是固定的O(log n);
MySQL BTREE索引使用的就是B+树存储,下面是一个BTREE索引大致结构:
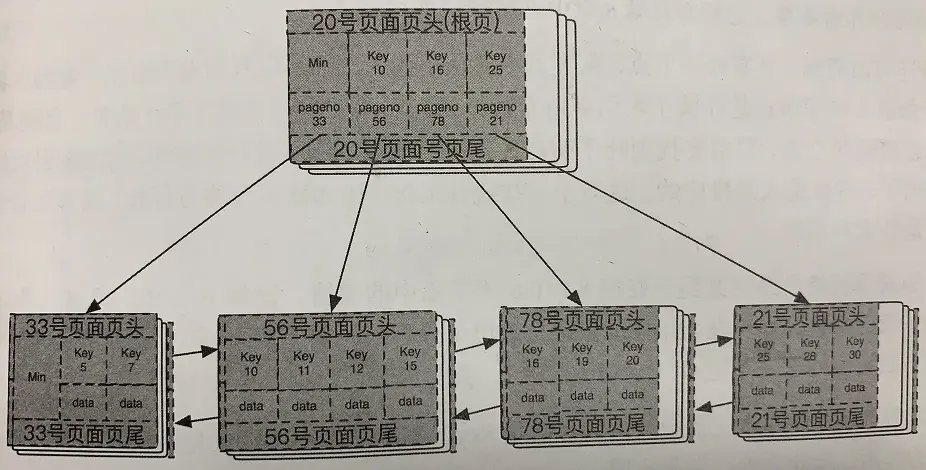
-
页号随机分布,逻辑上连续,但物理上并不是连续的。
-
在每一层的最左边节点页面的最左边位置,都有一个Min记录。
-
所有叶子节点,从左到右,从小到大,都是以双向链表链在一起的。
-
叶子结点中的data:
1.若是聚簇索引,则data存储除主键列之外的其他所有列组合;
2.若是二级索引,则data存储的就是这行记录对应的主键列组合,索引遍历时可根据此主键列进行回表查找。
二、聚簇索引和二级索引
聚簇索引
-
一个表中可以有多个索引,但每一个表都有一个索引是存储了所有数据的,这个索引一般被称为"聚簇索引"。
-
聚簇索引在一个表中只有一个,且是建立在主键上的,主键列可以是被隐藏的rowid列,也可以是自增列,还可以是定义的非空组合列等。
-
聚簇索引占用的空间是比较大的,因为索引包含行的所有列数据。
结构分类如下:自定义主键的聚簇索引 索引结构:【主键列】【TRXID】【ROLLPTR】【其他建表创建的非主键列】 参与记录比较的列:主键列 内结点Key列:【主键列】+PageNo指针未定义主键的聚簇索引索引结构:【ROWID】【TRXID】【ROLLPTR】【其他建表创建的非主键列】 参与记录比较的列:只ROWID一列而已 内结点Key列:【ROWID】+PageNo指针
二级索引
- 聚簇索引之外的所有索引都称为二级索引。
结构分类如下:自定义主键的二级唯一索引 索引结构:【唯一索引列】【主键列】 参与记录比较的列:【唯一索引列】【主键列】 内结点Key列:【唯一索引列】+PageNo指针自定义主键的二级非唯一索引 索引结构:【非唯一索引列】【主键列】 参与记录比较的列:【非唯一索引列】【主键列】 内结点Key列:【非唯一索引列】【主键列】+PageNo指针未定义主键的二级唯一索引 索引结构:【唯一索引列】【ROWID】 参与记录比较的列:【唯一索引列】【ROWID】 内结点Key列:【唯一索引列】+PageNo指针未定义主键的二级非唯一索引索引结构:【非唯一索引列】【ROWID】 参与记录比较的列:【非唯一索引列】【ROWID】 内结点Key列:【非唯一索引列】【ROWID】+PageNo指针
三、索引存储数据量估算
key数据存储量估算:
若每个页可以存1000个key,而且树的高度是4,那么
-
第一层页面,只有一个页,存储key 1000个;
-
第二层可以存储1001个页,相应的key就是 1000*1001;
-
第三层可以存储的1000*1001+1个页,相应的key就是1000*(1000*1001+1),约100亿条;
-
第四层为叶子结点,可以存储1000*(1000*1001+1)+1个页,每个页存储的数据量就会比内结点的1000少,因为有data部分,假设存256个,那么这个B+树存满的情况下,共可以存储(1000*(1000*1001+1)+1)*256条记录,2562,5625,6256,约2500亿条,估计mysql是没机会处理这么大数据量的单表了。
即使是千亿级别的数据量,要查找一个记录的话,也只需要4个页面的IO即可完成最终数据的定位,在叶子结点中,只需要做一次内存级的二分查找即可找到具体的数据记录。
四、索引插入过程
前提条件如下:
-
假设每个页面最多可以插入三条记录,插入第四条的时候就会发生分裂;
-
插入数据为键值时,但我们只关注键,值可以不用关注,就简单地以data代替即可;
-
插入的数据序列为:10,20,5,8,23,22,50,21,53,40,9;
-
为了简单明了一些,key就是一个简单的INT类型的数字;
-
假设根结点页面号为100。
插入步骤
步骤一
因为索引中还没有数据,所以此时的B+树只有一个空的根结点,又由于一个页只能存3个key,首先将10,20,5插入进去(实际上此步发生了3次插入),然后在页面内做数据排序,最终结果如下图:
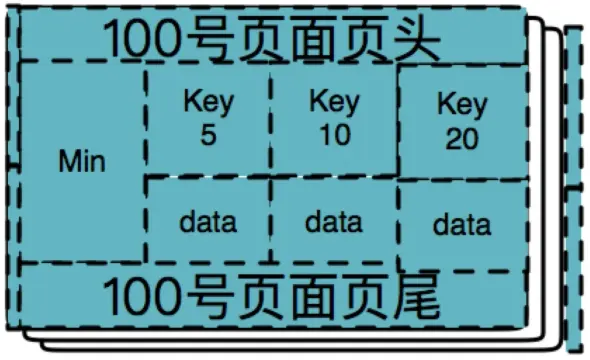
步骤二: 由于根页面已经写满,此时插入8,将发生分裂(根页面分裂),大致步骤如下:注意:在分裂过程中,根结点始终是不会变的,不管变成多大的树,根结点的页面号始终如一。
-
首先,创建一个新的叶子结点,假设申请的页面号是101。B+树的内结点和叶子结点实际上是通过不同的段来组织的,这里由于根结点同时还是叶子结点,里面存储的数据都是全部的数据,而不只是key,所以这里从叶子结点取,来创建一个新的叶子结点。
-
然后将原页面的全部记录复制到新页面中,原根页面的最小虚记录要指向新叶子结点,同时将原根页面中的记录全部删除;
-
最后将根页面的Min记录指针指向新的叶子结点101号页面,这样就构成一个B+树形结构了。如下图:
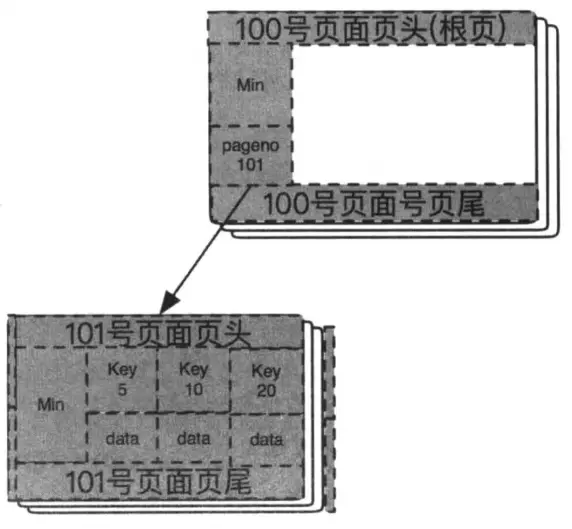 上面的分裂动作已完成,开始插入数据8,此时直接定位到叶子结点101号页面,在这个页面插入时发现还是没有空间,所以又涉及一次叶子结点的分裂,步骤如下:
上面的分裂动作已完成,开始插入数据8,此时直接定位到叶子结点101号页面,在这个页面插入时发现还是没有空间,所以又涉及一次叶子结点的分裂,步骤如下: -
首先,创建一个新的叶子结点,假设页面号是102;
-
将101号页面的一部分数据移到102号页面中,这里的一部分一般是指一半,这里可以假设每次移过去1条;
-
101和102号页面都是叶子结点,称为兄弟关系,他们需要组成双向链表;
-
将一半数据移到102号页面之后,此时这个页面需要需要与根结点挂上关系,要做的就是将20这条记录的key取出来,然后加上一个指针,组成一条新的记录插入到根页面中,如下两图:
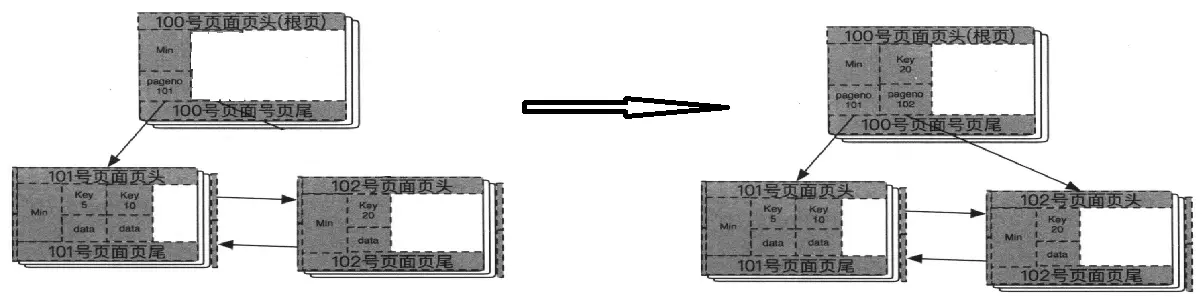 至此,所有的分裂准备工作都已完毕,终于可以插入数据8了。步骤很简单,从根结点开始搜索,8比20小,就从Min这个记录上找到对应的叶子节点,101号页面,然后执行插入,因为是排序的,所以插入到5和10之间(这是为了可以简单直白地看到,其实内部的排序组织不是这样的),这样,101号页面就有5、8、10三条记录了。如下图所示:
至此,所有的分裂准备工作都已完毕,终于可以插入数据8了。步骤很简单,从根结点开始搜索,8比20小,就从Min这个记录上找到对应的叶子节点,101号页面,然后执行插入,因为是排序的,所以插入到5和10之间(这是为了可以简单直白地看到,其实内部的排序组织不是这样的),这样,101号页面就有5、8、10三条记录了。如下图所示:
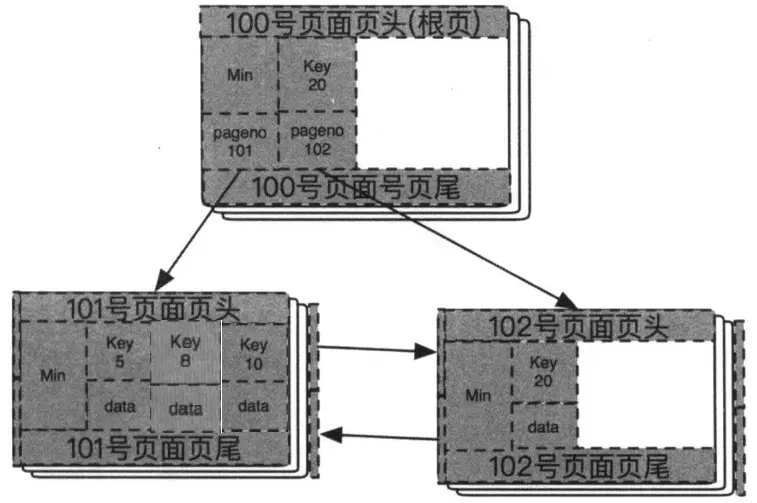
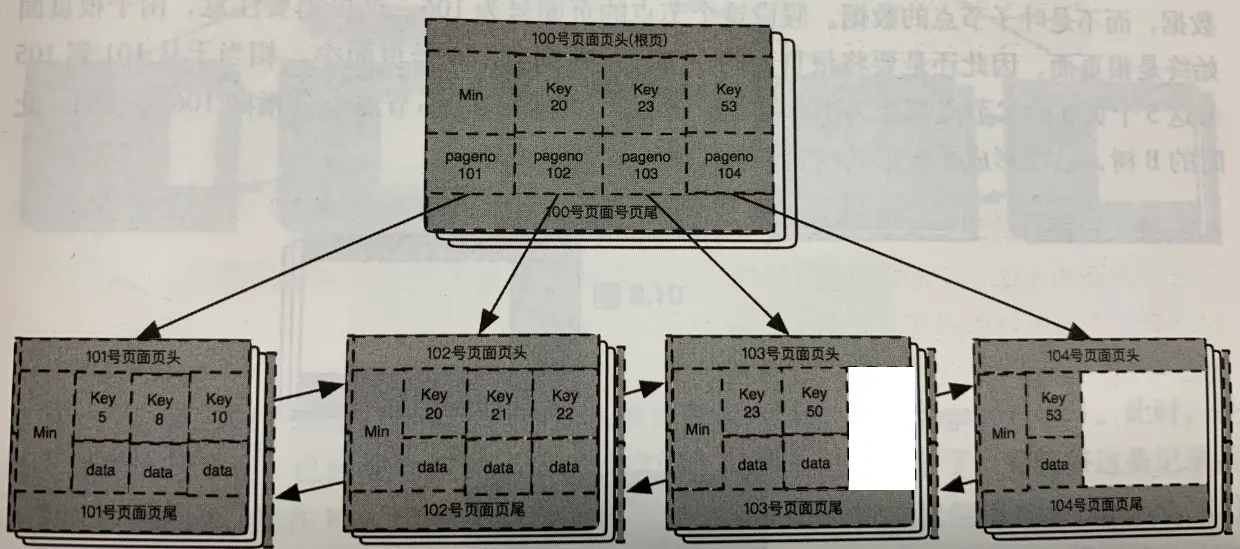
步骤三: 插入数据23、22,因为这个数据都是大于20的,所以找到相应的叶子节点102号页面执行插入,而且空间足够,所以直接插入这两条记录,插入后B+树结构如下图所示:
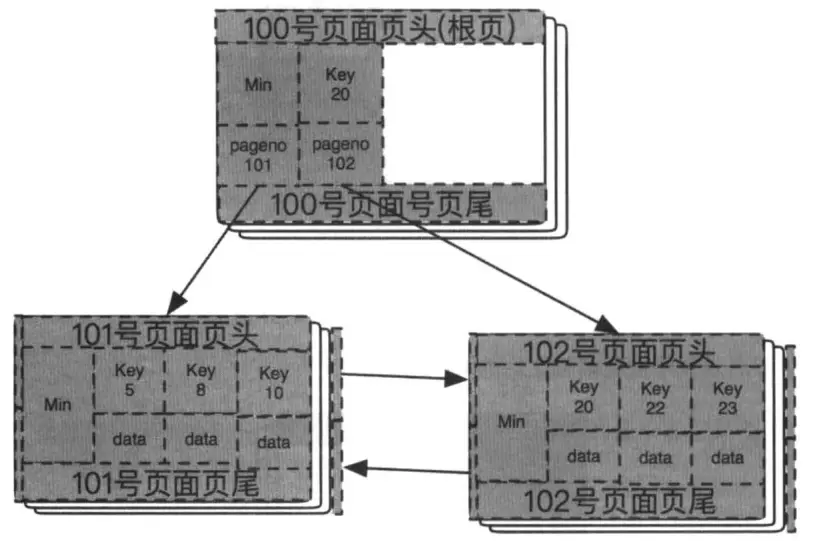
步骤四: 继续插入数据50,因为大于20,找到102号页面,发现页面已满,执行叶子结点的分裂,分裂同上面叶子结点的分裂步骤。分裂后如图所示:
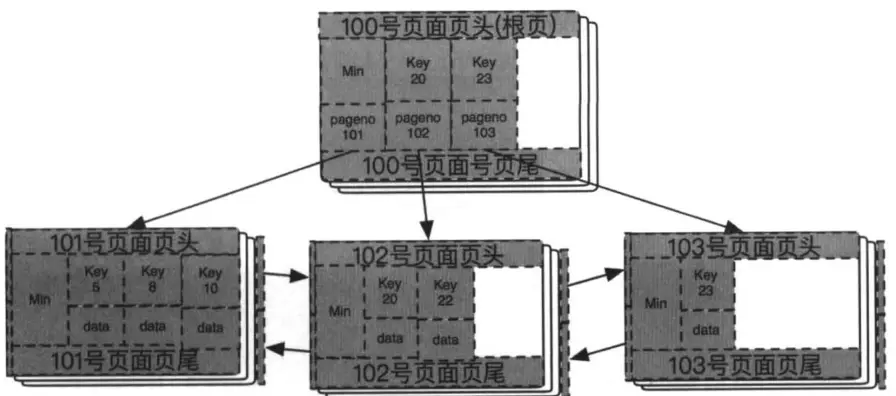 然后插入50
然后插入50
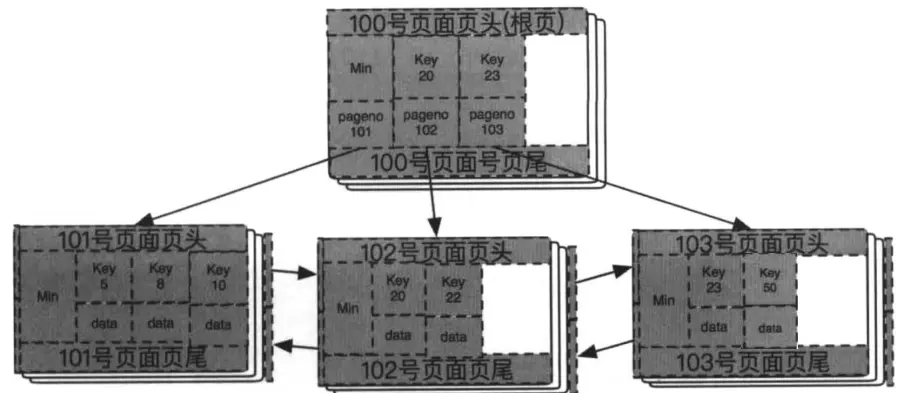 接着插入21
接着插入21
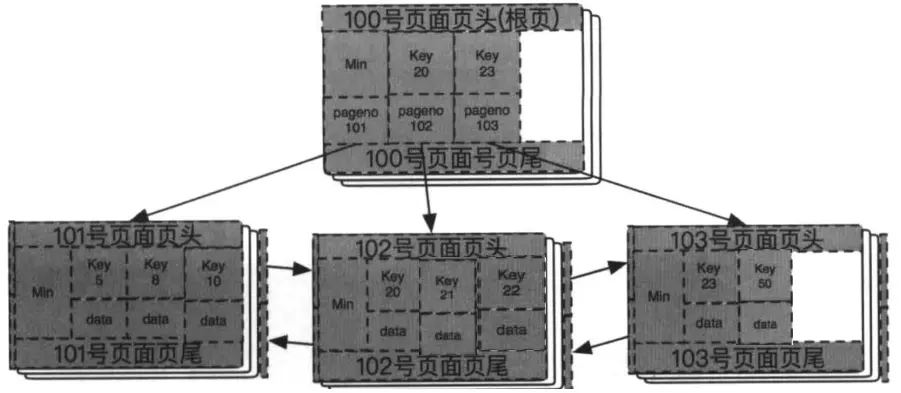 接着插入53
接着插入53
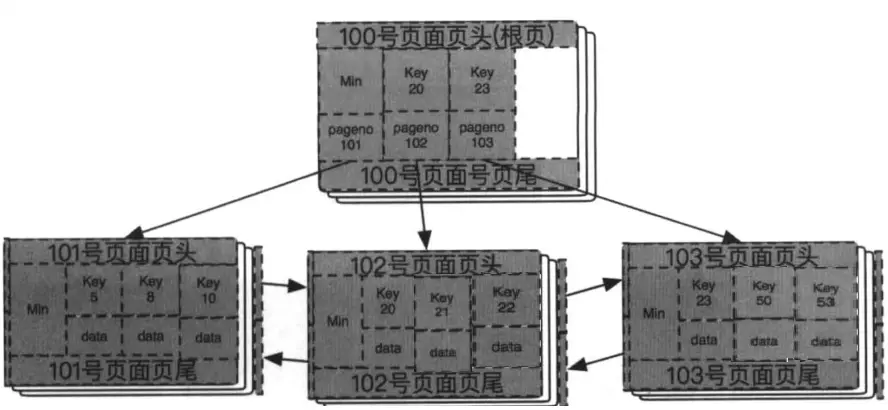 此时叶子结点均已写满,下次数据插入必将产生分裂。
此时叶子结点均已写满,下次数据插入必将产生分裂。
步骤五:
插入数据40,发现比根结点23大,找到103号页面,发现已满,执行分裂,分裂同上面叶子结点的分裂步骤。分裂后如图所示:
 插入40:
插入40:
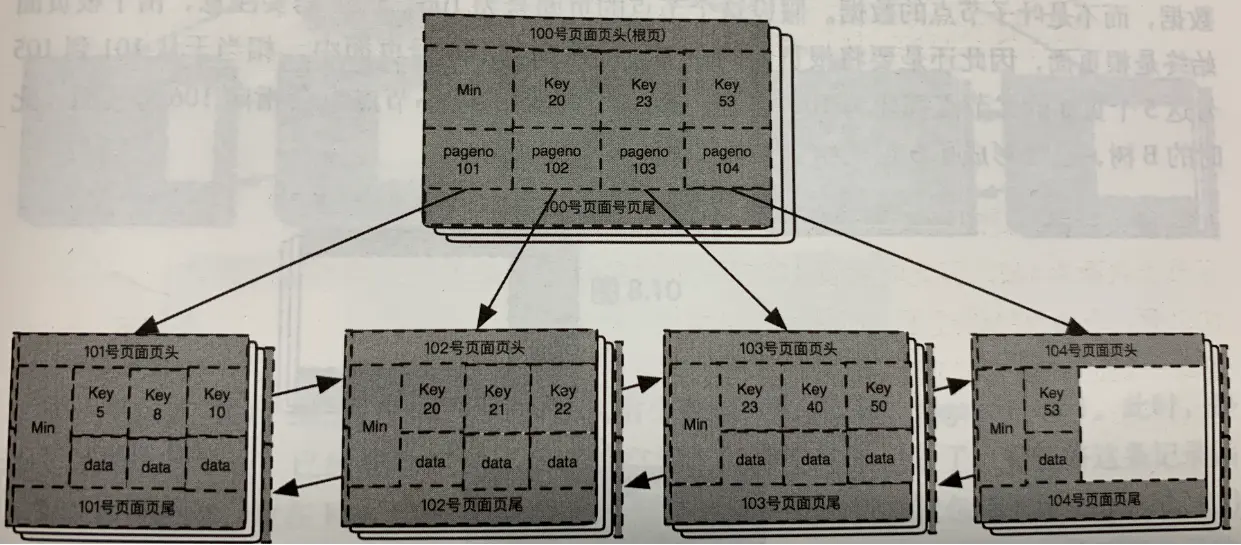
步骤六:
继续插入下一个数据9,因为比20小,找到101号页面,发现已满,需要做叶子结点分裂,如下图:
 叶子节点分裂之后,需要与根结点产生父子关系,但是不幸,根结点也已满,需要做根页面的分裂。新建一个结点106,将根结点100号页面的数据复制过去,而根结点100始终是根结点,如下图所示。
叶子节点分裂之后,需要与根结点产生父子关系,但是不幸,根结点也已满,需要做根页面的分裂。新建一个结点106,将根结点100号页面的数据复制过去,而根结点100始终是根结点,如下图所示。
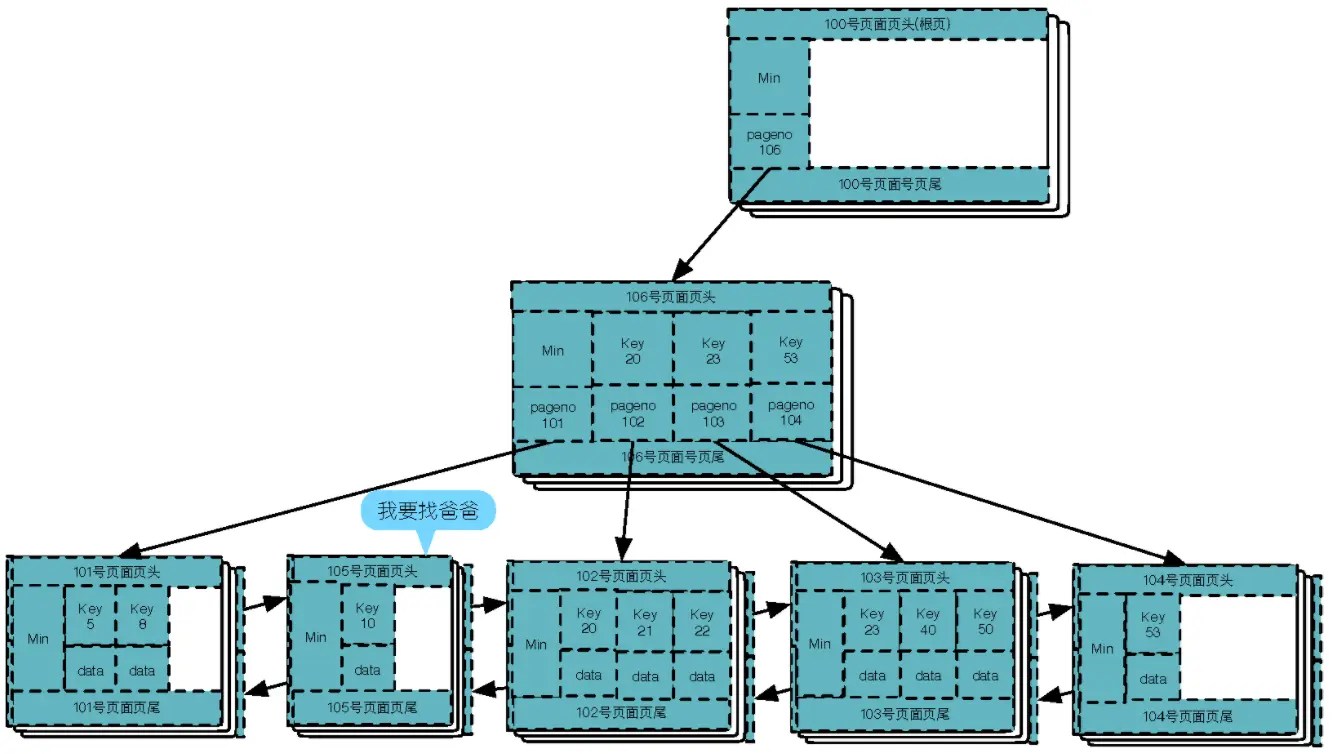 此时106号页面还是满的,key 10 还是无法写到内结点106上,需要做一次内结点分裂,新建内结点107号页面,分裂后如下图:
此时106号页面还是满的,key 10 还是无法写到内结点106上,需要做一次内结点分裂,新建内结点107号页面,分裂后如下图:
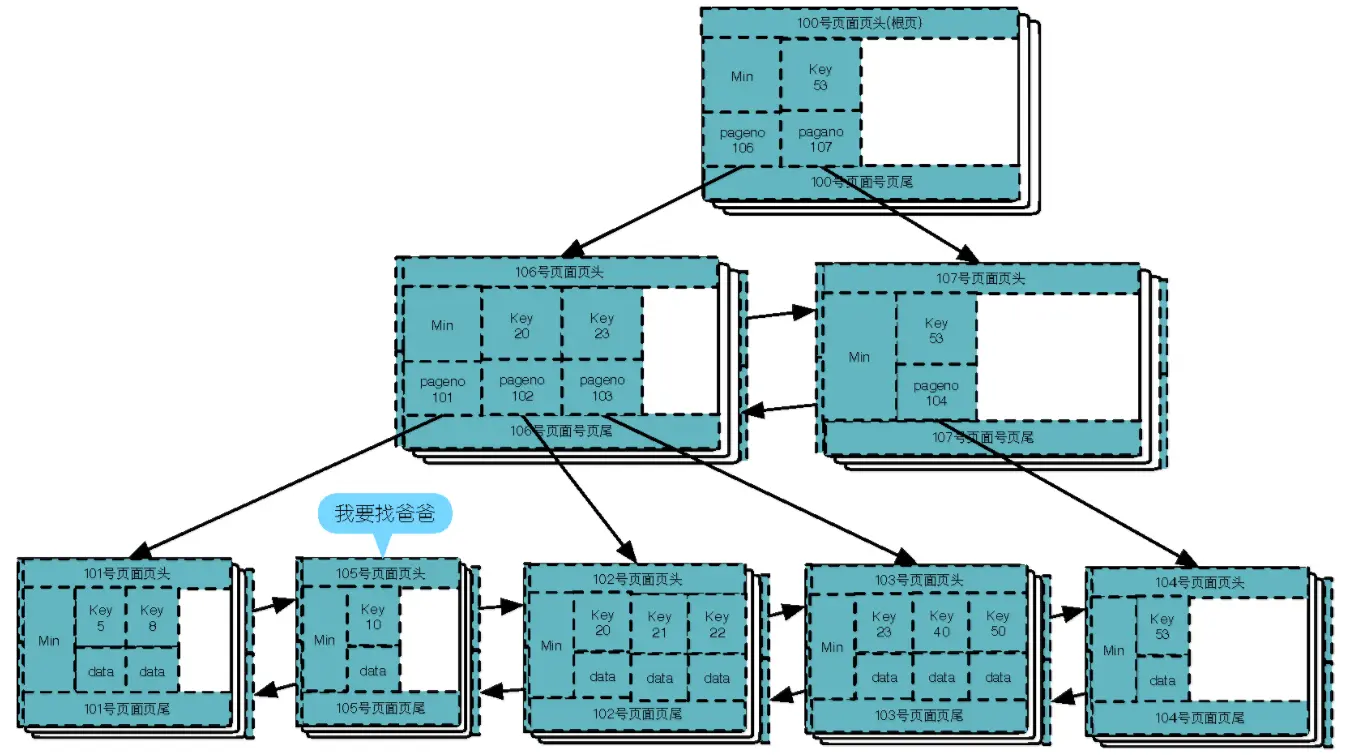 分裂后105号页面就可以找到自己的爸爸了,如下图:
分裂后105号页面就可以找到自己的爸爸了,如下图:
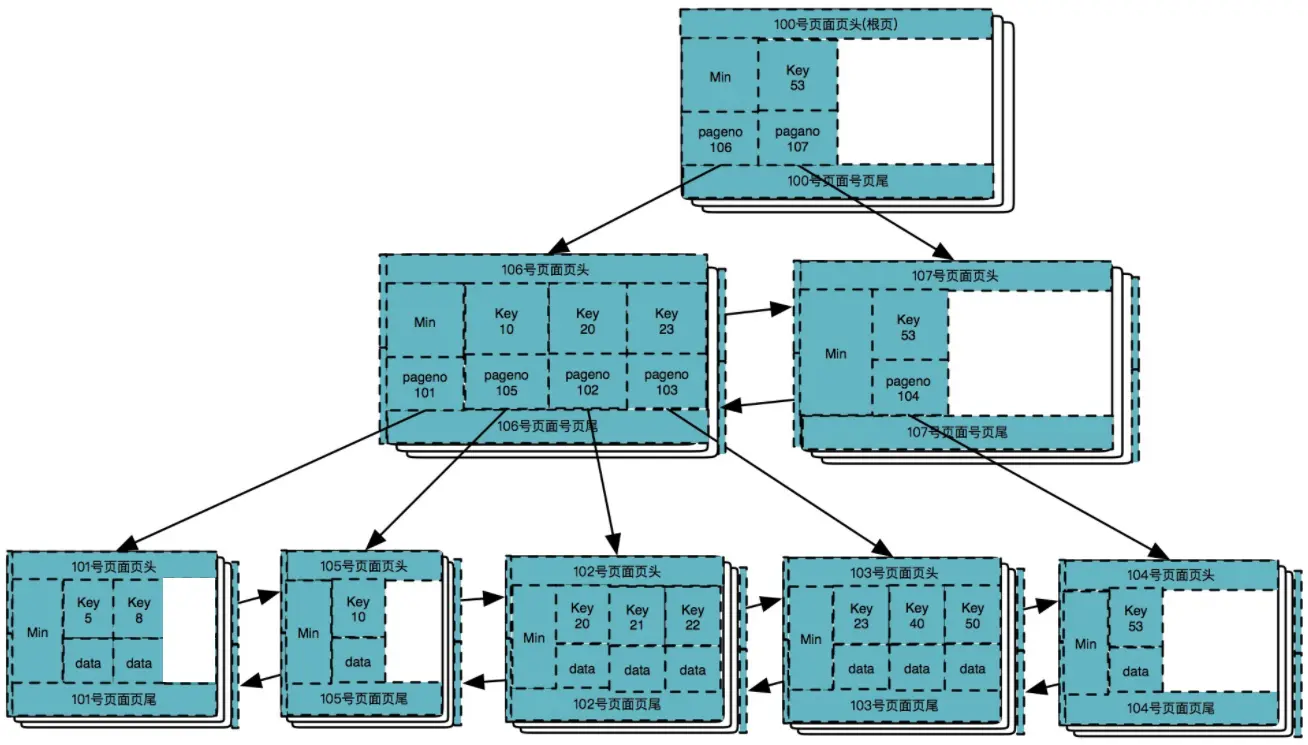 此时,只是完成了分裂,数据9还没有完成插入操作,此时很明显,插入时找到页面101执行插入即可,完成后如下图所示:
此时,只是完成了分裂,数据9还没有完成插入操作,此时很明显,插入时找到页面101执行插入即可,完成后如下图所示:
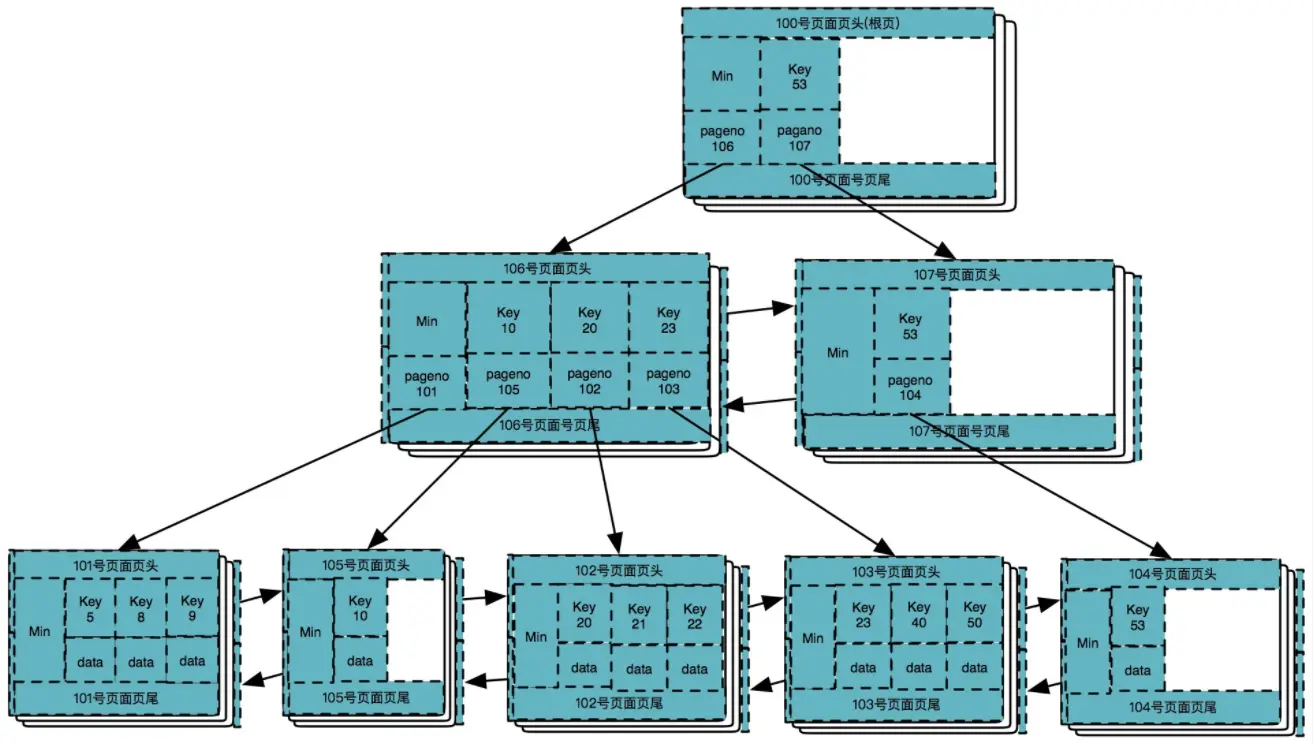 至此,所有的数据插入操作已经完成。
至此,所有的数据插入操作已经完成。
五、索引页面回收
传统B+树的数据删除,一般都会有一个所谓的填充因子,来控制页面数据的删除比例,如果数据量小于这个填充因子所表示的数据量,就会有节点合并,这与分裂是相对应的。 InnoDB的实现与传统B+树算法有不同之处,InnoDB在删除索引数据时,会先检查当前页剩余的记录数,如果只剩下一条记录,就会直接将这个页面从B+树中摘除,也只有这种情况,InnoDB才会回收一个页面,InnoDB的页面没有合并一说,但是对于根节点,即使索引数据全部删除,根节点页依然存在,只不过是以空页的形式存在。 下面举个例子描述索引删除过程,前提条件与前面插入记录时一致。
假设初始B+树如下(为上面插入完成后的B+树):
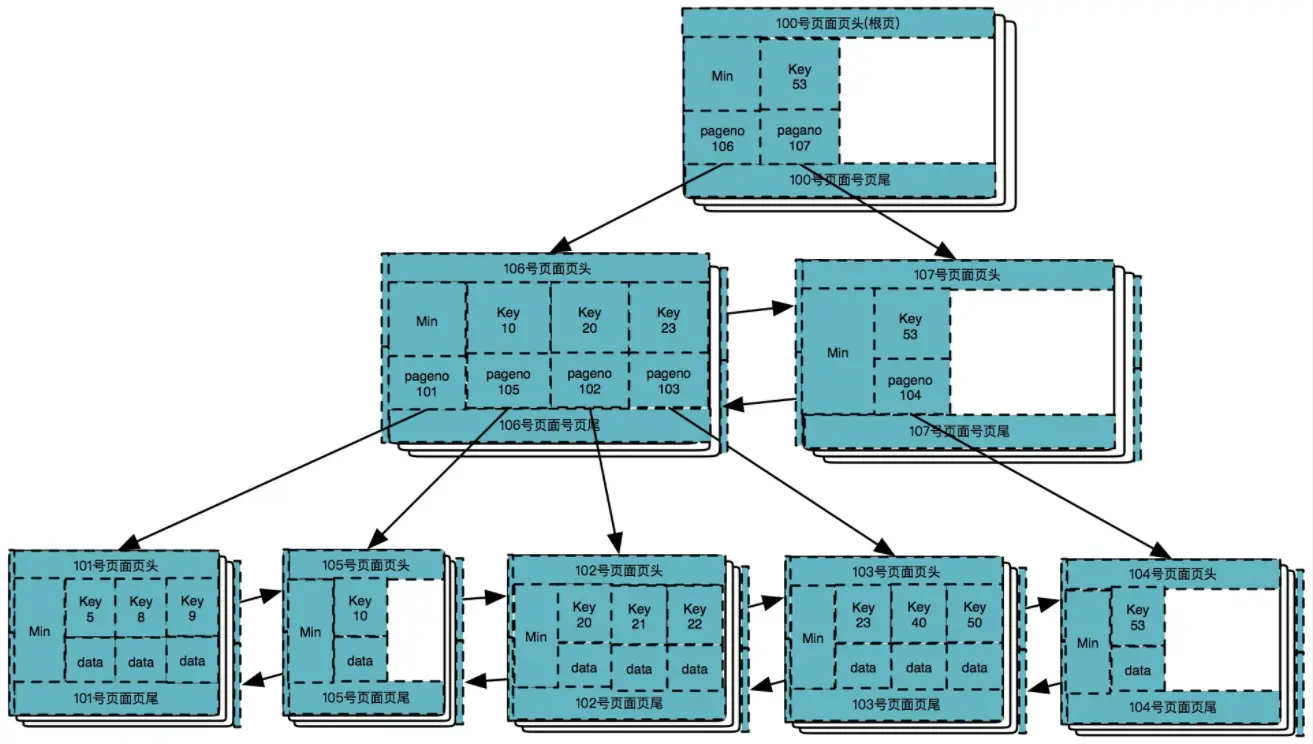
删除数据 50
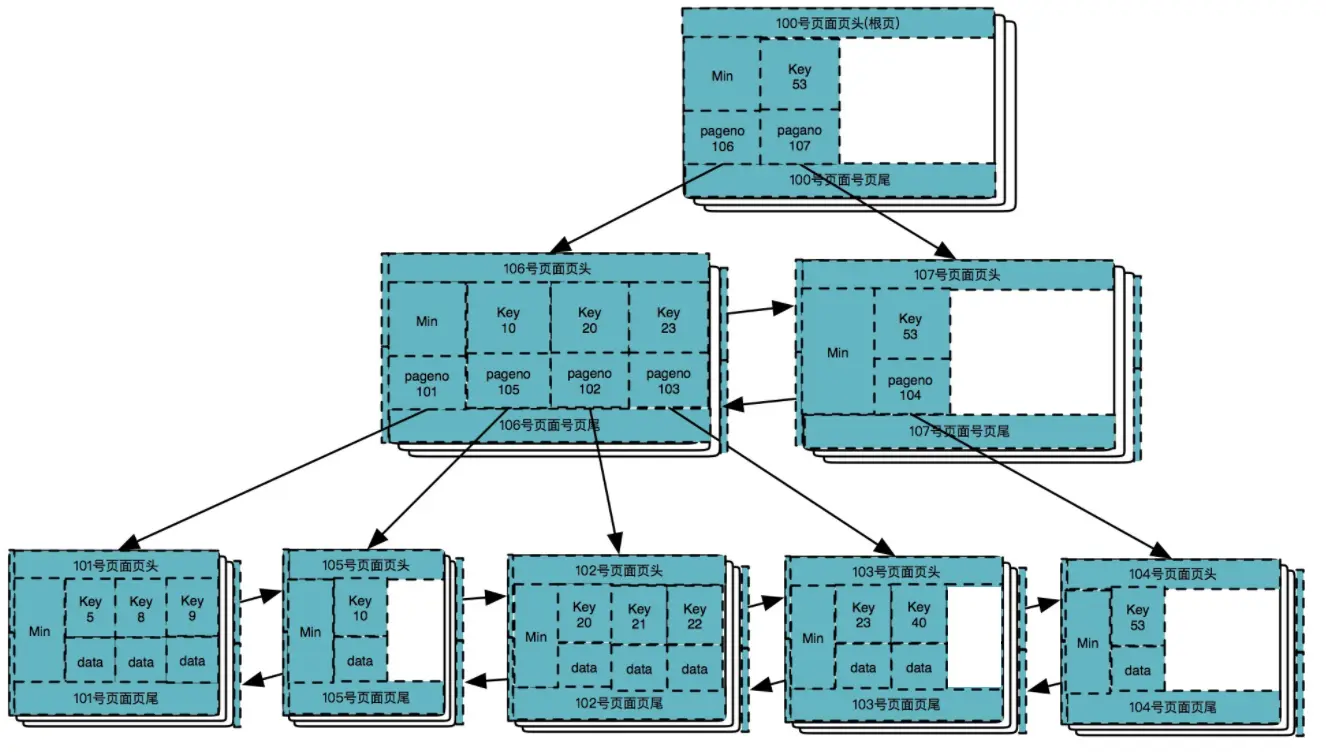
删除数据 20
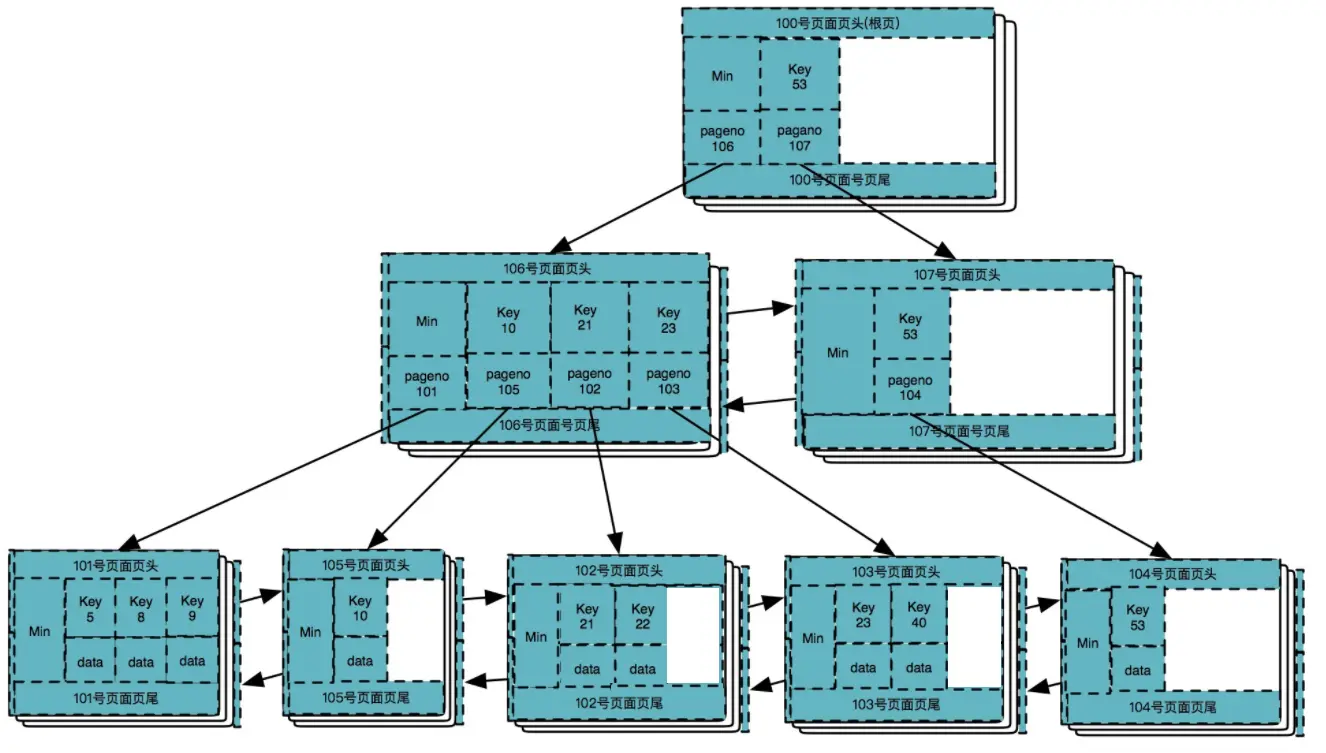
删除数据 10
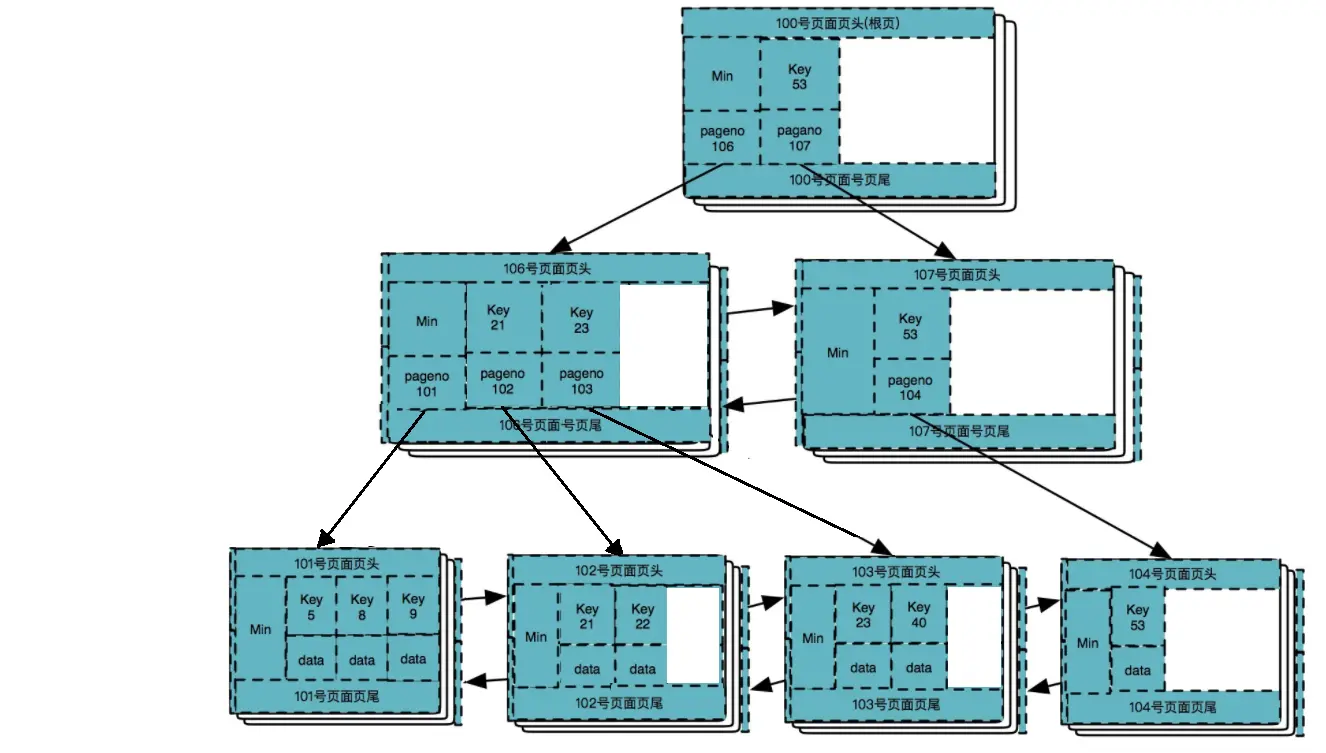
删除数据 23
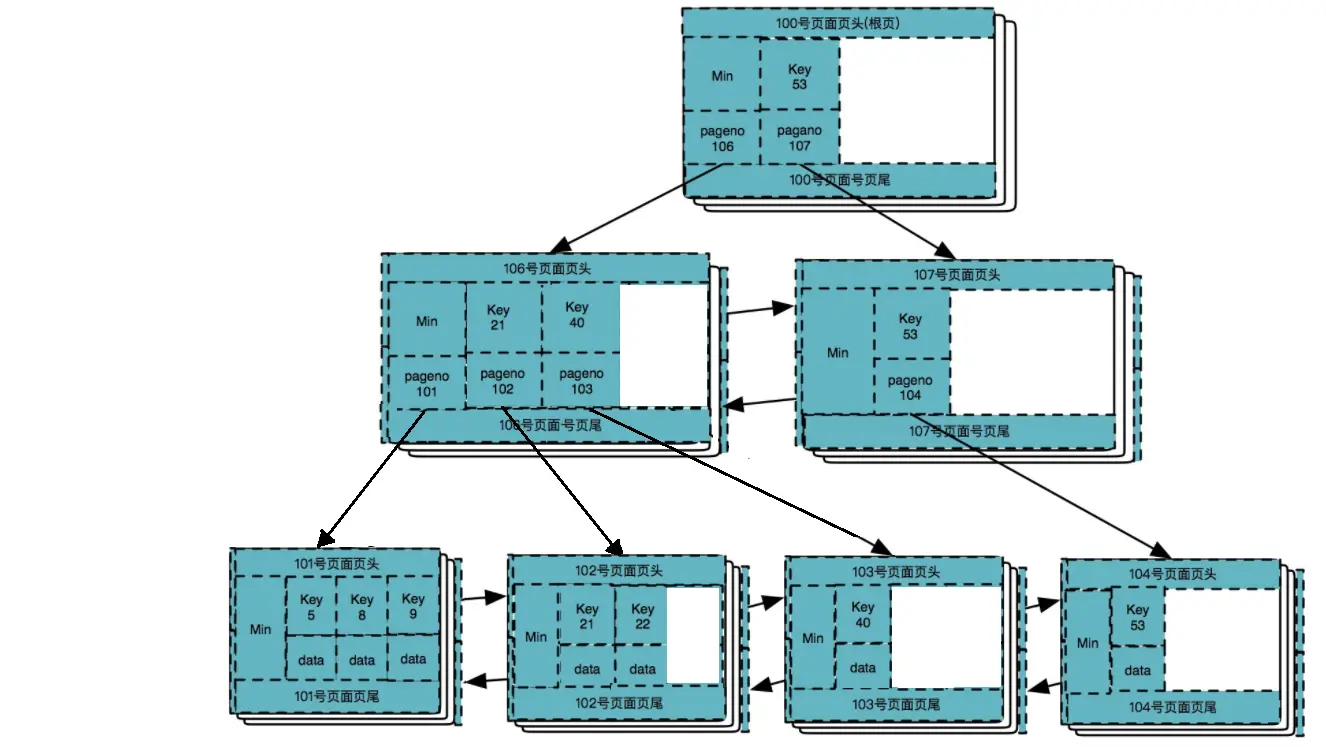
删除数据 40
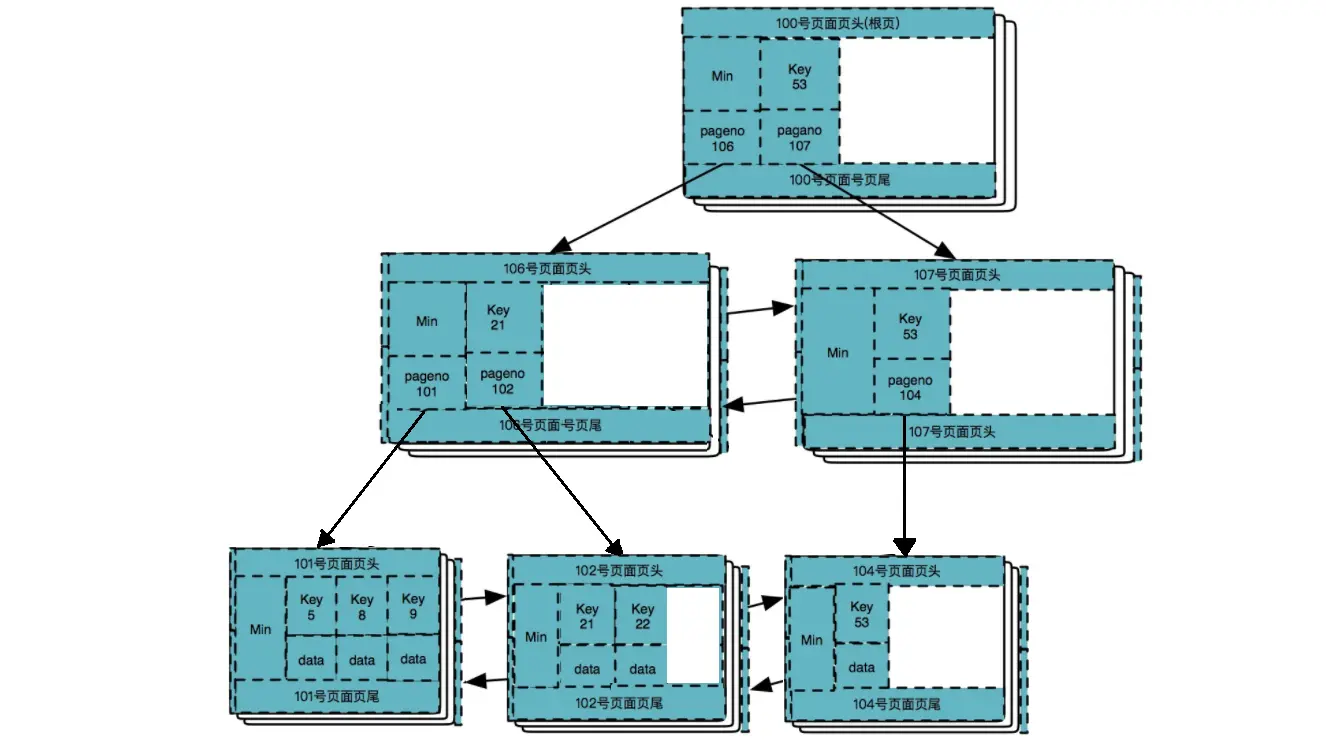
删除数据 53
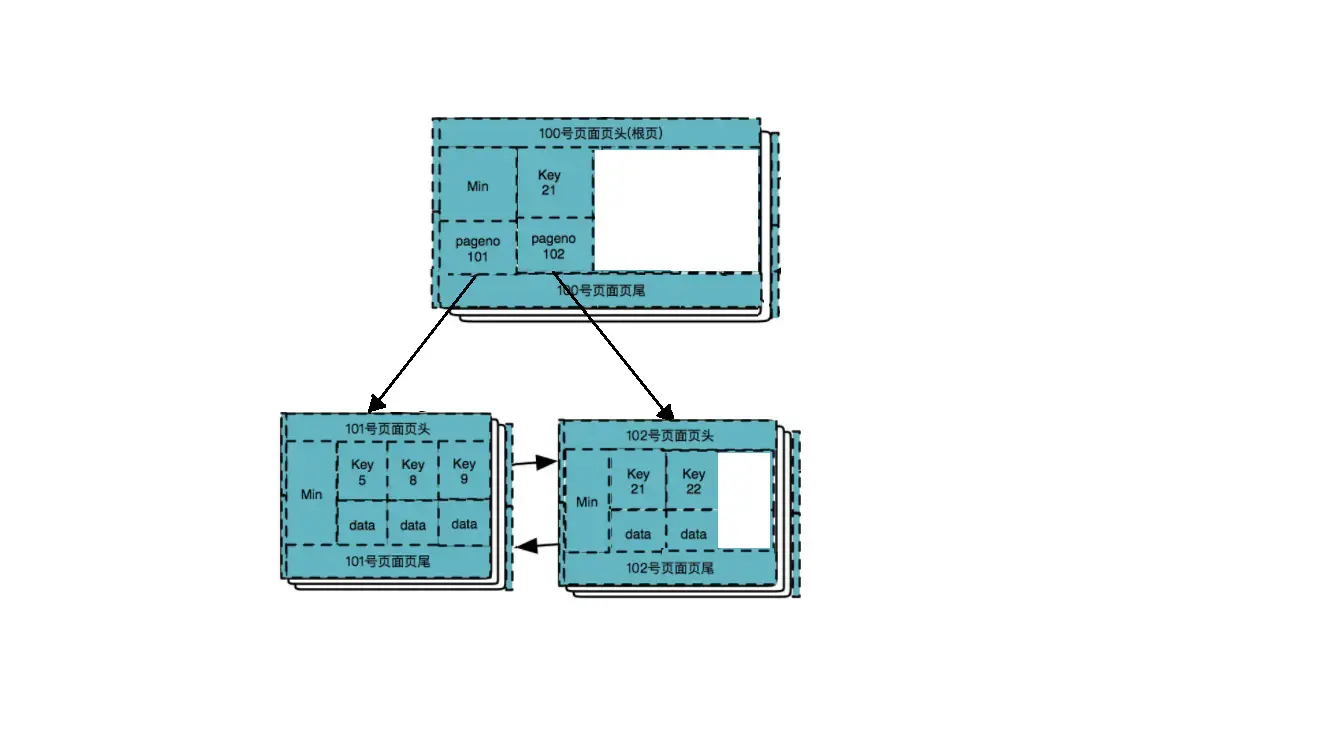
删除数据 8,9,21
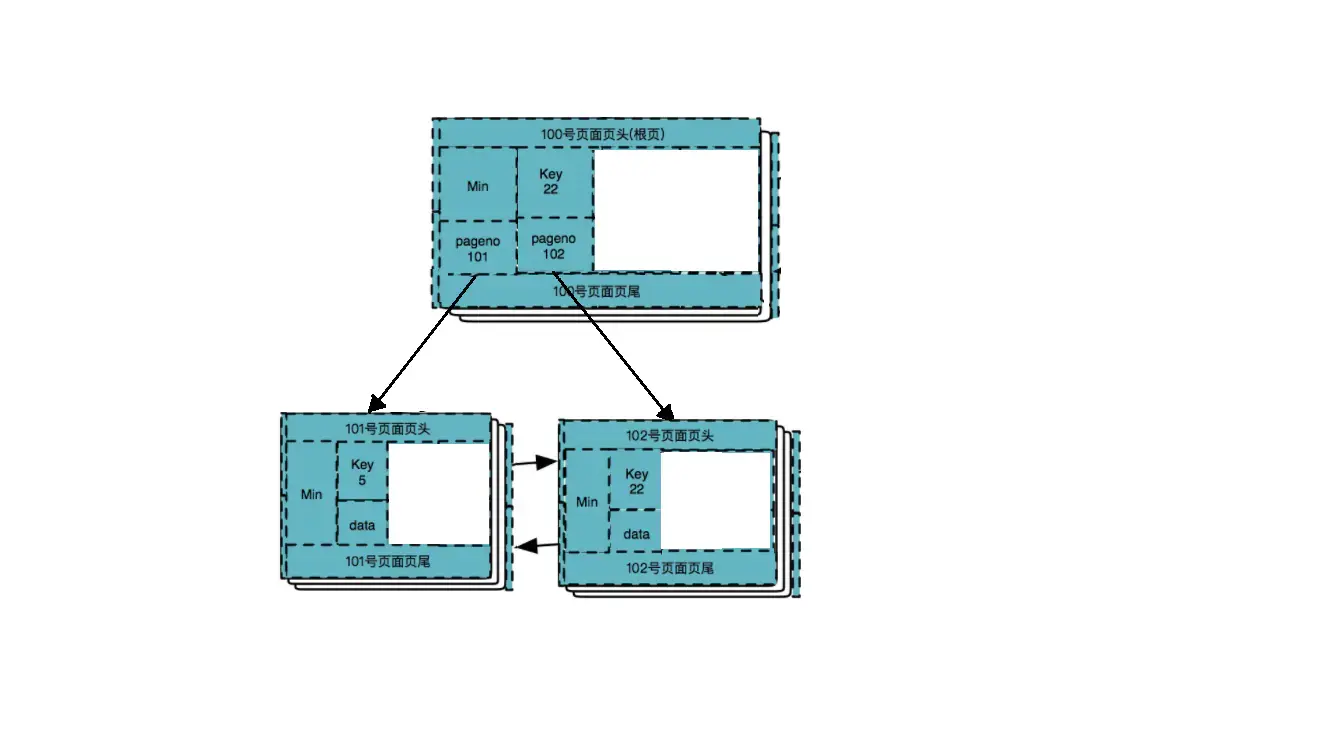
删除数据 5
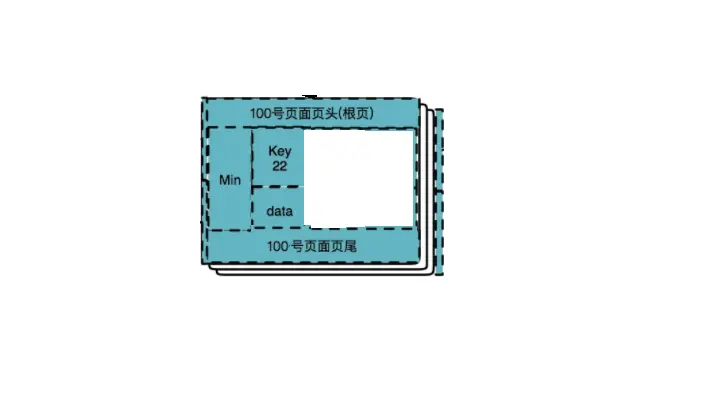
删除数据 22
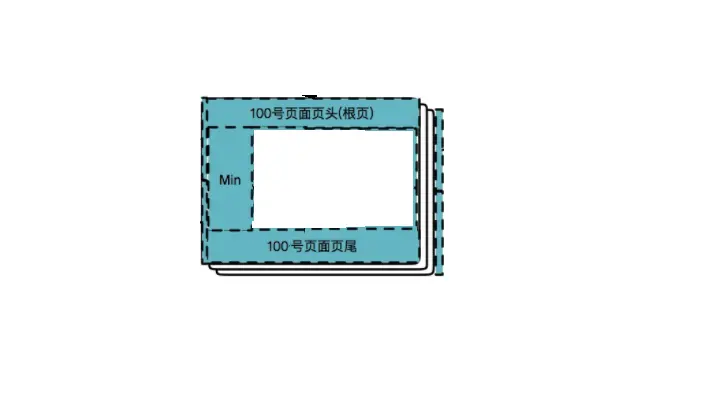
删除过程全部结束,最终得到一个空的索引页。
六、参考文档
《MySQL运维内参》
B+树动画演示:https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html
 51工具盒子
51工具盒子