在 1969 年 7 月 20 日，阿波罗登月舱着陆月球，第一位踏上月球的美国宇航员 Neil Armstrong，在出舱时说了一句经典："这是一个人的一小步，也是人类的一大步。"

当时，全球约有 6.5 亿观众通过电视直播见证了 Neil Armstrong 在月球上迈出第一步，其中就包括 17 岁的美国高中生 Jim Storer------自那时起， 他便产生了编写一款登月模拟程序的想法。

于是同年 11 月，Jim Storer 学会了 PDP-8（一款迷你电脑）特有的编程语言 FOCAL，用不到 50 行的代码写出了第一个"登月（Lunar Lander）游戏"。由于技术限制，这个"登月游戏"只能以文字呈现。

总体而言，"登月游戏"的内容很简单，就是由玩家扮演的宇航员需要手动操控一个登月器，目标是在月球上实现软着陆：

（1）每隔 10 秒钟，屏幕上会显示一行报告，统计飞船的高度、降落速度，以及剩余的燃料总量；

（2）报告结尾是一个空格，玩家要输入 0-200 之间的一个数字，决定接下来 10 秒内的燃料消耗量；

（3）登月舱需以一个极低的速度接触到月球表面，游戏才会提示"完美着陆"，期间若撞上障碍物、以高速撞击天体表面或耗尽燃料，游戏便会结束。

尽管这款游戏只是一个简单的文字游戏，没有画面、也没有声音，这也并不影响它在 1973 年成为当时"最受欢迎的计算机游戏"，并在后来有了许多衍生版本，风靡了近半个世纪。

近期，一名退休的软件工程师 Martin C. Martin 也玩上了这个游戏，想要探索最优燃料方案以实现软着陆，但他在深入研究游戏中复杂的物理和数值计算后发现：这个 55 年前开发的游戏，有一个至今都没人发现的 Bug！

要求软着陆，却从硬着陆变成完全没有着陆？

根据 Martin 的个人介绍，他自小学六年级起就开始编程，是卡内基梅隆大学机器人研究所的研究生，又成为了麻省理工学院的博士后。毕业之后，他曾在 Meta 工作，也曾在 Rockstar Games New England 担任 AI 主管。

已经退休的的他，近来在闲暇时间开始研究"登月游戏"的最佳方案：在确保安全着陆的前提下， 如何保留最多的剩余燃料。而他惊讶地发现，从游戏中推算出的最佳策略并不符合实际：缺少了一个"除以二"的操作，导致游戏错误地认为已经着陆的登月器还没有触地。

从游戏规则来看，为了在着陆时使用最少的燃料，玩家需要在最短的时间内完成着陆。理想方案是：最初，玩家可以通过关闭发动机来最大限度地提高速度，然后在最后一秒全速燃烧，正好在接触地面时把速度降为零------Kerbal Space Program 社区把这种方法称为"自杀式燃烧"，因为准确掌握时机非常难，且没有任何误差空间。

话虽如此，通过一些反复试验和手动二分查找，还是能找到一种恰好让登月器着陆的燃烧计划：在前 70 秒不燃烧任何燃料，然后在接下来的 10 秒内以每秒 164.31426784 磅的速率燃烧燃料，之后再以每秒 200 磅的最大速率燃烧：

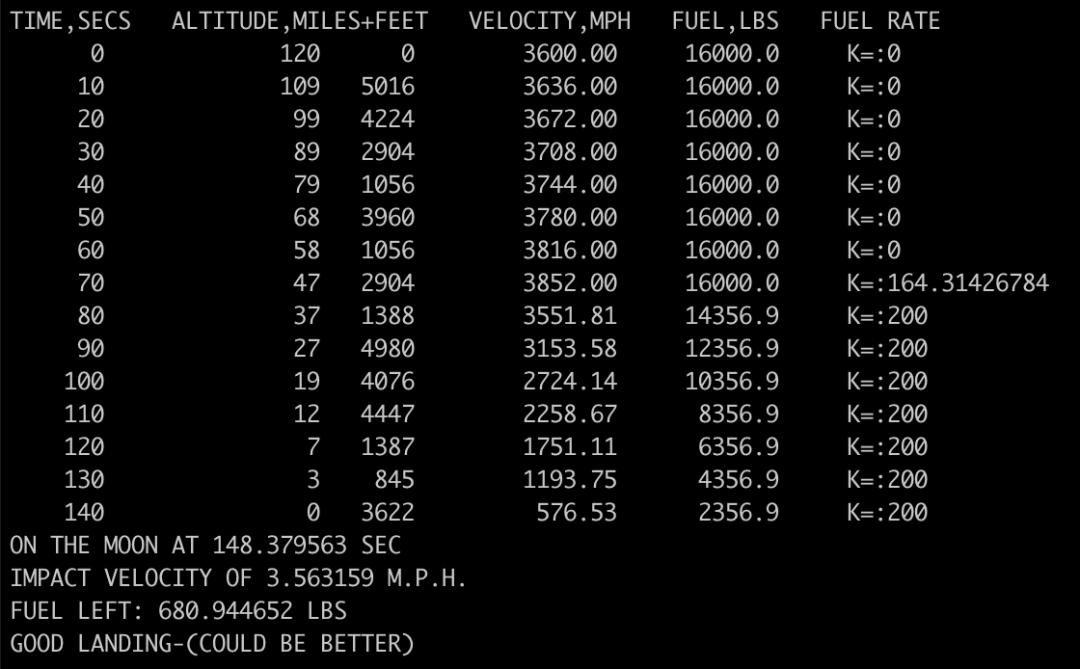
"登月游戏"中认为，完美着陆的速度应小于 1 英里/小时，但在这种情况下，我们以超过 3.5 英里/小时的速度着陆，游戏还提示说"可以做得更好"？然而实际情况是，哪怕每秒再多燃烧 0.00000001 磅的燃料，玩家也会完全错过地面，并以 114 英里/小时的速度上升：

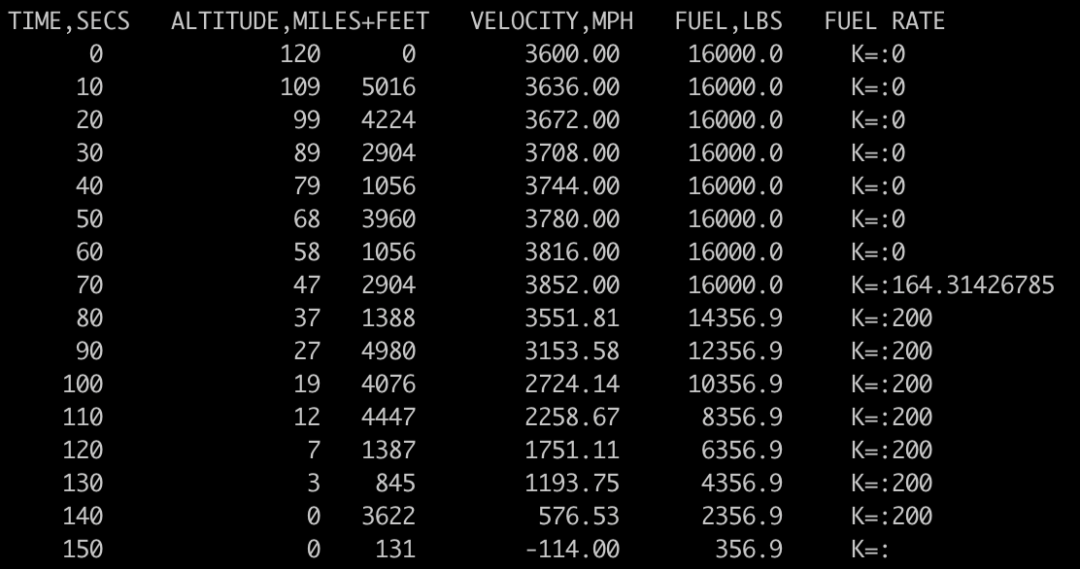
基于此，Martin 提出一个疑问："我们是如何从硬着陆变成完全没有着陆，且中间没有一个软着陆的过程呢？"

接触地面后，方案失效

Martin 本以为，会在这个"登月游戏"中看到一种在如今电子游戏中依然很常见的欧拉积分，也就是在每个时间步（timestep）开始时计算力，然后使用公式 F=ma 计算加速度，再假设加速度在 Δt\Delta tΔt 秒的时间步内保持恒定：

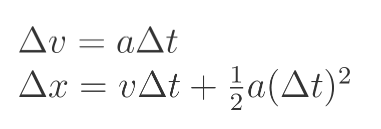
由于质量在时间步内不断变化，加速度也会随之变化，所以假设加速度为常数只是一个近似值。

但令人惊讶的是，游戏作者 Jim Storer 使用了精确的解决方案，即齐奥尔科夫斯基火箭方程，并用泰勒展开式对其对数进行计算。此外，Jim Storer 还用了一些代数方法来简化计算，减少了四舍五入的误差。对于在 1969 年还是高中生的他来说，这已经非常了不起了。

当 Martin 问他这个问题时，Jim Storer 回答道："当时我已经熟练掌握微积分、泰勒级数等概念，而且在我的印象中，身为物理学家的父亲还在我推导这些方程时帮了我。"

知晓 Jim Storer 设计游戏的方法后，Martin 很快就懂了：因为用的是火箭方程，所以"自杀式燃烧"成为了最优选择，而且 Jim Storer 使用泰勒级数的五个项，在参数最大为 0.1212 时，可以达到超过六位小数的精度，所以这"不是我们要找的问题所在"。

理论上来说，在登月舱触地之前火箭方程的效果确实很好------但 Martin 指出，等接触地面后这个方法就不成立了，而这也是登月游戏面临的最大挑战。

"想象一下，登月舱在一个 10 秒的回合中开始时下降，但到回合结束时上升。仅仅验证它在这两个时间点都在地表上方是不够的，因为它可能在中间的某个时刻低于地表。当这种情况发生时，程序必须回溯并检查之前的某个时刻。"

有一个显而易见的方法，就是查看轨迹的最低点，即速度为零的时刻。对于火箭方程而言没有一个合适的表达式来表示这个最低点，因此可以使用物理学家最喜欢的技巧，只取泰勒级数的前几项。如果只使用对数的前两项，问题就简化成了一个二次方程，你可以用高中学过的经典二次方程来求解公式。在 10 秒的回合内，这个近似值应该相当不错，精确度在 0.1% 左右。

但 Martin 发现 Jim Storer 不是这么做的：在他的公式中，平方根在分母而不是分子，另外误差也放大了 30 倍。

"他少了平方根内分母中的 2！"

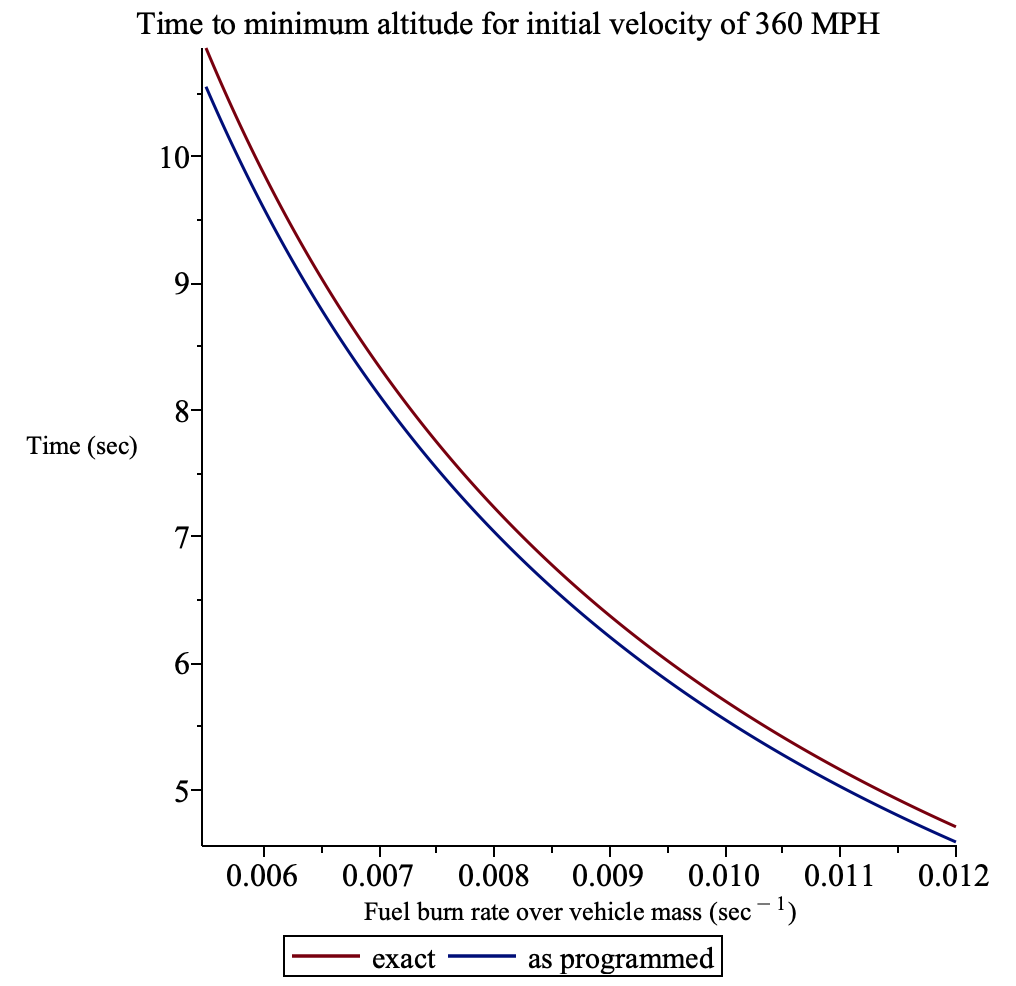
Martin 研究了 Jim Storer 的公式很久，发现怎么算也不会涉及平方根。直到他更仔细地看了看 Jim Storer 的平方根，它的形式是：

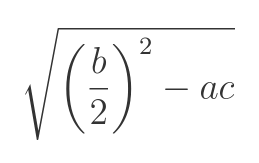
这看起来很像是在平方根内除以 4 的二次方程式，但为什么会在分母上呢？在尝试了一些方法后，Martin 重新发现了一个二次方程的替代形式，其中平方根在分母上，也与 Jim Storer 代码中的公式相符。

尽管如此，Martin 依旧不知道为什么 18 岁的 Jim Storer 要用这种替代形式。也许他重新推导了二次方程公式，而不是查阅现有公式，结果推导出了这种形式？也许他担心会出现灾难性的抵消（catastrophic cancellation），所以想用正数相加而不是相减的形式？

但是，如果他的公式是等价的，那为什么近似误差会高出 30 倍呢？

Martin 尝试自己推导公式，得到了以下结果："这与 Jim Storer 的公式几乎完全相同，只是......他少了平方根内分母中的 2！"

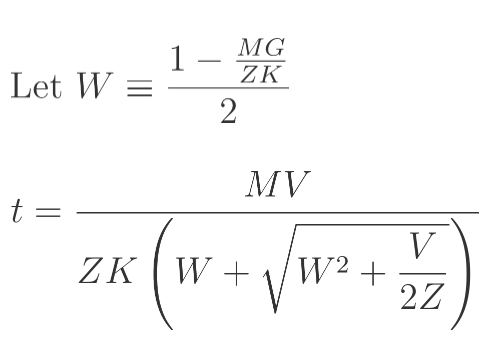
Martin 指出，这可能是推导公式或输入计算机时的一个简单错误。毕竟，当时的计算机代数系统 MACSYMA 仅在 Jim Storer 开发前一年才开始使用，并且在 Jim 的高中并不可用，所以他必须用铅笔和纸完成所有工作。

由于这个 Bug，Jim Storer 始终低估了到达最低点所需的时间。他可以通过两种方式来补偿：增加 0.05 秒，然后从新的、更接近的位置重新估算。这也就解释了为什么会错过着陆时间：第一次估算是在登月舱还在地表上方并持续下降时，第二次估算是在登月舱到达最低点并再次上升之后，而这不到 0.05 秒。

接下来，如果把缺失的 2 倍系数加上并去掉 0.05，会发生什么呢？现在，"自杀式燃烧"所能达到的最佳效果是：速度降到了 1.66 英里/小时，离 1 英里/小时的完美着陆还有将近四分之三的距离。

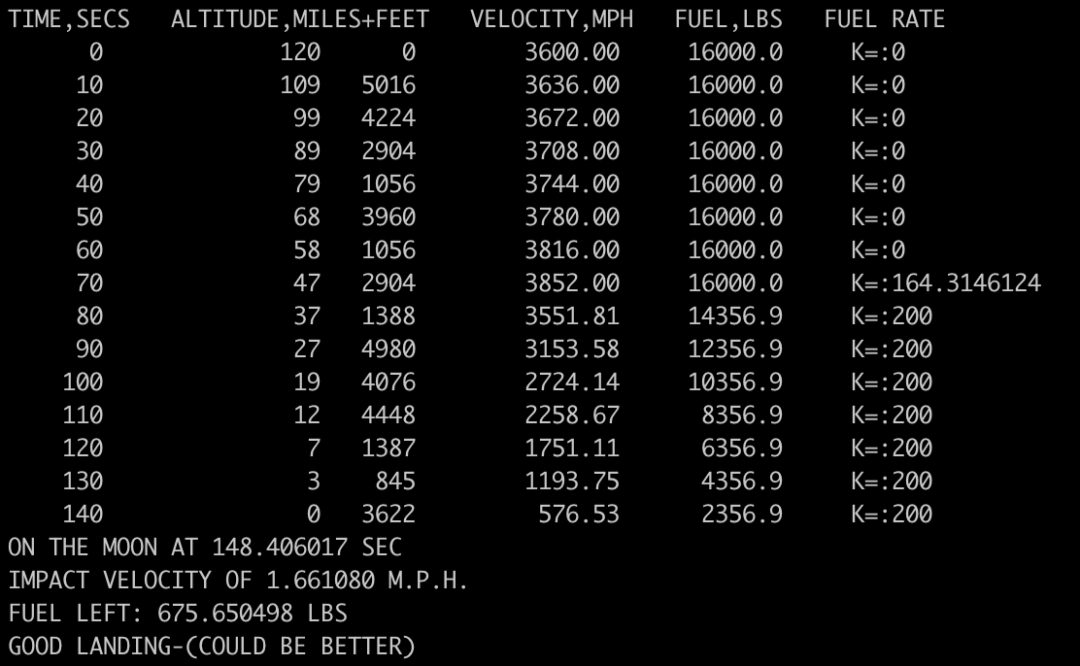
这并不完美，因为我们仍然只使用了泰勒级数的前两项。另外，一旦确定最低点是在地面下，就需要找到首次撞击地面的时间，这就会涉及到类似的近似计算。平缓着陆也是可行的，只需在第 14 个回合结束时降低高度和速度，然后在第 15 个回合中使用低推力，150 秒后在某处着陆即可。Martin 补充道，他无法理解的只是理论上的全推力着陆自杀式燃烧，大约需要 148 秒。

即使有这个 Bug，这仍是一个有趣的游戏

最后 Martin 评价称，对于 1969 年使用 PDP-8 的 17 岁高中生来说，Jim Storer 的这个登月游戏已经是一个非常了不起的作品了。

毕竟，当时的高中还没有计算机科学课程，数值计算方面的知识也并不是谁都知道的------甚至 Martin 自己，也是攻读机器人学博士学位时才学到这些知识。令 Martin 惊讶的是，这个错误已经存在了将近 55 年，而之前却没有人注意到它。

不过，对此 Martin 也表示理解：即使有这个 Bug，这仍然是一个有趣的游戏。"不仅要赢，还想找到最佳策略，这种追求自然会让人们试图理解微小的差异。我想其他人都只是乐于玩这个游戏，并从中获得乐趣。"

参考链接：https://martincmartin.com/2024/06/14/how-i-found-a-55-year-old-bug-in-the-first-lunar-lander-game/