算法1------穷举法 {#算法1——穷举法}

def method_of_exhaustion(lst):
	length = len(lst)
	this_sum = max_sum = 0
	for i in range(length):
		for j in range(i, length):
			this_sum = 0
			for k in range(i, length):
				this_sum += lst[k]
			if this_sum > max_sum:
				max_sum = this_sum
	return max_sum

第一种算法是最容易也是最容易懂的一种算法，算法的核心思想很简单，就是穷举所有的可能解，然后通过比较返回最优解

算法分析 {#算法分析}

第一层循环的索引i表示子序列左端的位置，第二层循环表示子列右端位置，第三层循环计算该子列的大小

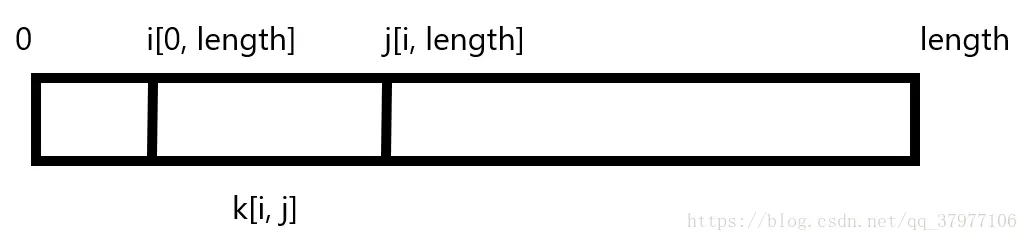
从示意图可以看到，i从0遍历到length(数组的长度)，j从遍历到length，在j的每一趟中，最内层循环都要从i到j计算一次子序列的大小，其实这是完全没必要的，假设数组a在i的某趟中，j + 1时的子序列的值为a[j] + a[j + 1]，即j的前一个子序列的值加上当前索引j在数组中的值。由此衍生出第二个算法。

时间复杂度分析 {#时间复杂度分析}

1、直观的看可以看到函数中有三个循环，所以时间复杂度为O(N^3)。

2、精确的分析来看，该函数是由三重嵌套for循环组成的，最外层的循环次数为N = length，即数组的长度。
第2个循环大小为N - i，它可能要小，但也可能是N。

我们必须假设最坏的情况，而这可能会使最终的界有些大。

第3个循环的大小为j - i + 1我们也要假设它的大小为N。因此总数为O(1 · N · N · N) = O(N^3)
第2行和和3行总共的开销只是O(1)，而语句6和10也只不过总共开销O(N^2)，因为它们只是两层循环内部的简单表达式。

3、更精确的分析来看，考虑到这些循环的实际大小，更精确的分析指出答案是Θ(N^3)，而在我们上面的估计高6倍（不过这并无大碍，因为常数不影响数量级）。一般来说，在这类问题中上述结论是正确的。精确的分析由和\sum_{i=0}^{N-1}\sum_{j=i}^{N-1}\sum_{k=i}^{j}1得到，该"和"指出程序的第14行被执行多少次。首先有：
\sum_{k=i}^j 1 = j - i + 1
接着，得到
\sum_{j=i}^{N-1} (j - i + 1) = \frac{(N - i + 1)(N - i)}{2}
这个和是对前N - i个整数求和而计算得出的。为完成全部计算，我们有
\sum_{i=0}^{N-1} \frac{(N - i + 1)(N - i)}{2} = \sum_{i=1}^N \frac{(N - i + 1)(N - i + 2)}{2}
= \frac{1}{2}\sum_{i=1}^N i^2 - (N + \frac{3}{2})\sum_{i=1}^N i + \frac{1}{2}(N^2 + 3N + 2)\sum_{i=1}^N 1
=\frac{1}{2}\frac{N(N + 1)(2N + 1)}{6} - (N + \frac{3}{2})\frac{N(N + 1)}{2} + \frac{N^2 + 3N + 2}{2}N
=\frac{N^3 + 3N^2 + 2N}{6}

算法2------优化版穷举法 {#算法2——优化版穷举法}

def optimized_method_of_exhaustion(lst):
	length = len(lst)
	this_sum = max_sum = 0
	for i in range(length):
		this_sum = 0
		for j in range(i, length):
			this_sum += lst[j]
			if this_sum > max_sum:
				max_sum = this_sum
	return max_sum

第二种算法是在第一个算法的基础上去掉了重复计算子序列大小的循环

时间复杂度分析 {#时间复杂度分析-1}

和算法1类似地可以知道算法2的时间复杂度为O(N^2)。

算法3------分治法 {#算法3——分治法}

def divide_and_conquer(lst, left, right):
	if left == right:
		if lst[left] > 0:
			return lst[left]
		else:
			return 0
center = (left + right) // 2
# 左边界最大子序列和右边界最大子序列
max_left_sum = divide_and_conquer(lst, left, center)
max_right_sum = divide_and_conquer(lst, center + 1, right)

max_left_border_sum = left_border_sum = 0
for i in range(center, left -1, -1):
	left_border_sum += lst[i]
	if left_border_sum > max_left_border_sum:
		max_left_border_sum = left_border_sum

max_right_border_sum = right_border_sum = 0
for i in range(center + 1, right + 1):
	right_border_sum += lst[i]
	if right_border_sum > max_right_border_sum:
		max_right_border_sum = right_border_sum

# 左、右与跨越边界的子序列
return max(max_left_sum, max_right_sum, max_left_border_sum + max_right_border_sum)

算法分析 {#算法分析-1}

分治法是一种使用广泛的算法，其基本思想是："如果整个问题比较复杂，可以将问题分化，各个击破"。分治包含"分"和"治"两个过程，先将问题分成两个大致相等的子问题，然后递归地对它们求解。

在此例中，先将序列等分成左右两份，最大子序列只可能出现在三个地方：

1. 整个子序列出现在左半部分；
2. 整个子序列出现在右半部分；
3. 跨越左右边界出现在中间。

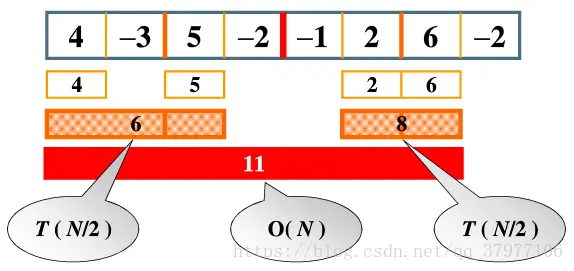
前两种情况可以通过递归地从中间向两边累加得到，第三种情况可以将左部分最大和和右部分最大和及他们中间的元素相加得到。在代码中表现在第10行、第11行和第26行中的max的第三个参数，第26行返回的是三者中最大的子序列。

疑问1 ：代码中的max_left_sum(max_right_sum)和max_left_border_sum(max_right_border_sum)有什么区别？
答 ：max_left_sum(max_right_sum)是递归求出来的边界左边的最大子序列，但是它不一定是挨着边界的，而max_left_border_sum是从边界延伸向左边的最大子序列。


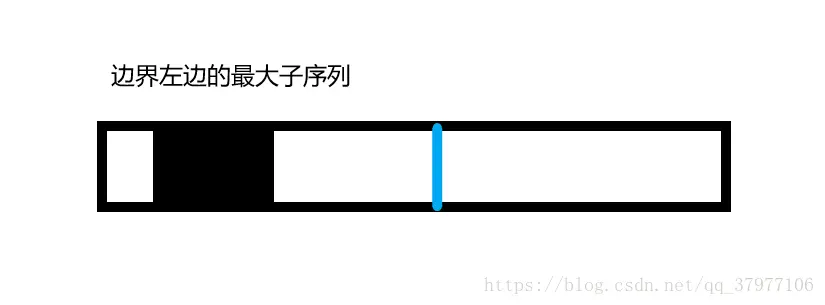
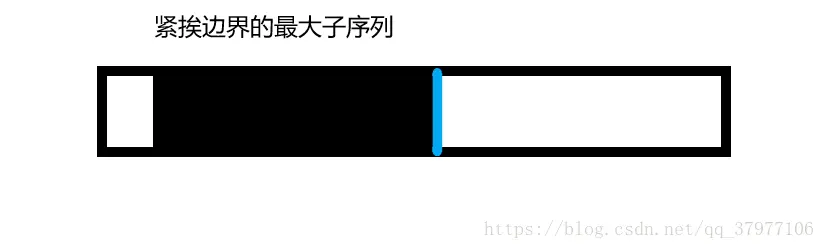
紧挨左边界的最大子序列与紧挨右边界的最大子序列相加就能得到跨越边界的最大子序列。

时间复杂度分析 {#时间复杂度分析-2}

令T(N)是求解大小为N的最大子序列和问题所花费的时间。
从代码中可以看到，第2~8行、第13行与第26行花费的时间为常量，即O(1)；
第15行和第16行的规模减半，分别为T(\frac{N}{2})，共花费2T(\frac{N}{2})个时间单元；
第14行~17行与第20~23行的循环中，两者循环次数相加为N，花费O(N)个时间单元。
总花费的时间为2T(\frac{N}{2}) + O(N)，得到方程组：

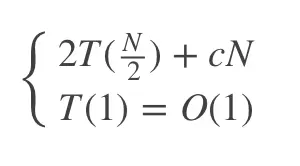
T(N) = 2T(\frac{N}{2}) + cN

递归使N / 2 并代入T(\frac{N}{2})

=2[2T(\frac{N}{2^2}) + c\frac{N}{2}] + cN

递归除以2直到，当N除以k次2时，\frac{N}{2^k} = 1，此时为递归的终点，即使得代码中的left=right。一直递归展开，中括号外将会乘以k个2，即2^k，T(\frac{N}{2^k})最终变成T(1) = O(1)，中括号内的2 · c\frac{N}{2}加上外面的cN一共是k个cN，即

=2^kO(1) + ckN 其中\frac{N}{2^k} = 1

=O(N logN)

算法4------在线算法 {#算法4——在线算法}

def online_algorithm(lst):
	length = len(lst)
	this_sum = max_sum = 0
	for i in range(length):
		this_sum += lst[i]
		if this_sum > max_sum:
			max_sum = this_sum
		elif this_sum < 0:
			this_sum = 0
	return max_sum

算法分析 {#算法分析-2}

在理解这个算法之前，首先要知道最大子序列的两端的元素（或者连续子序列，整个子序列可以看作是一个元素）是不可能为负的，因为如果为负，总是会有通过将这个负的元素（或连续子序列）去掉而使子序列和更大。

在线算法从0开始累加，当累加到i时，若\sum_{0}^{i}lst[i] < 0，则可以将[0, i]这一段看作是最左端的小于0的连续子序列，此时[0, i]这一段便可以舍弃，并从i开始重新累加，当累加到某个值j时又小于0，则舍弃[i, j]这一段继续从j开始重新累加。

该算法附带的一个优点是，它只对数据进行一次扫描，一旦lst[i]被读入并被处理，它就不再需要被记忆。因此，如果数组在在磁盘上或通过互联网传送，那么它就可以被按顺序读入，在主存中不必存储任何部分。不仅如此，在任意时刻，算法都能对它已经读入的数据给出子序列问题的正确答案。具有这种特性的算法叫做在线算法(on-line algorithm)，或联机算法。仅需要常量空间并以线性时间运行的在线算法几乎是完美的算法。

时间复杂度分析 {#时间复杂度分析-3}

显而易见，该算法以线性时间运行，时间复杂度为O(N)

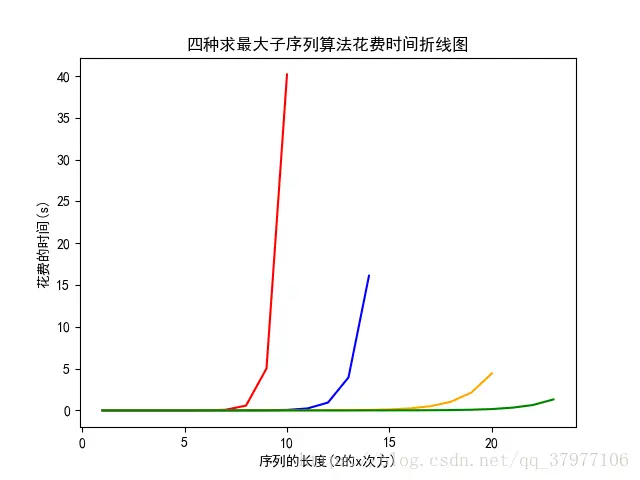
四种算法在实际运行中的表现 {#四种算法在实际运行中的表现}

图中第一个算法当数组个数仅为1024个(2^{10})时就已经达到了40s，所以我在这里加入了一个控制语句，当x > 10时第一个算法不再运行，第二个与第三个分别控制在2^{14}和2^{20}不再运行；而在线算法在数组个数达到8388608个(2^{23})时所花费的时间仍不超过3s。

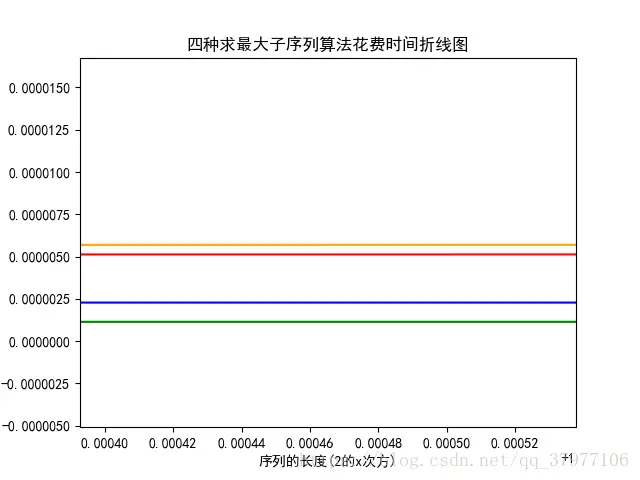
将折线图前面的部分放大可以看到，其实分治法(橙色)运行的时间是要比前两种算法运行的时间花费的更多的，这可能是因为在python中调用函数花费的时间比执行少数的语句所花费的时间要长。

完整的python代码（运行时间一分钟左右） {#完整的python代码（运行时间一分钟左右）}

import timeit
from random import randint
import matplotlib.pyplot as plt
import progressbar
method_of_exhaustion_time_list = []
optimized_method_of_exhaustion_time_list = []
divide_and_conquer_time_list = []
online_algorithm_time_list = []
x_values = []
生成指定长度的范围为[-1000, 1000]的整数列表
def generate_integer_list(length = 10):
lst = []
for i in range(length):
lst.append(randint(-1000, 1000))
return lst
穷举法
def method_of_exhaustion(lst):
length = len(lst)
this_sum = max_sum = 0
for i in range(length):
for j in range(i, length):
this_sum = 0
for k in range(i, length):
this_sum += lst[k]
if this_sum > max_sum:
max_sum = this_sum
return max_sum
穷举法优化
def optimized_method_of_exhaustion(lst):
length = len(lst)
this_sum = max_sum = 0
for i in range(length):
this_sum = 0
for j in range(i, length):
this_sum += lst[j]
if this_sum > max_sum:
max_sum = this_sum
return max_sum
分治法
def divide_and_conquer(lst, left, right):
if left == right:
if lst[left] > 0:
return lst[left]
else:
return 0
center = (left + right) // 2
# 左边界最大子序列和右边界最大子序列
max_left_sum = divide_and_conquer(lst, left, center)
max_right_sum = divide_and_conquer(lst, center + 1, right)

max_left_border_sum = left_border_sum = 0
for i in range(center, left -1, -1):
	left_border_sum += lst[i]
	if left_border_sum > max_left_border_sum:
		max_left_border_sum = left_border_sum

max_right_border_sum = right_border_sum = 0
for i in range(center + 1, right + 1):
	right_border_sum += lst[i]
	if right_border_sum > max_right_border_sum:
		max_right_border_sum = right_border_sum

# 左、右与跨越边界的子序列
return max(max_left_sum, max_right_sum, max_left_border_sum + max_right_border_sum)

在线处理
def online_algorithm(lst):
length = len(lst)
this_sum = max_sum = 0
for i in range(length):
this_sum += lst[i]
if this_sum > max_sum:
max_sum = this_sum
elif this_sum < 0:
this_sum = 0
return max_sum
四种算法时间测试
def test(lst):
time_list = []
if len(lst) < 2 ** 11:
	start = timeit.default_timer()
	method_of_exhaustion(lst)
	end = timeit.default_timer()
	method_of_exhaustion_time_list.append(end - start)
else:
	method_of_exhaustion_time_list.append(None)

if len(lst) < 2 ** 15:
	start = timeit.default_timer()
	optimized_method_of_exhaustion(lst)
	end = timeit.default_timer()
	optimized_method_of_exhaustion_time_list.append(end - start)
else:
	optimized_method_of_exhaustion_time_list.append(None)

if len(lst) < 2 ** 21:
	start = timeit.default_timer()
	divide_and_conquer(lst, 0, len(lst) - 1)
	end = timeit.default_timer()
	divide_and_conquer_time_list.append(end - start)
else:
	divide_and_conquer_time_list.append(None)

start = timeit.default_timer()
online_algorithm(lst)
end = timeit.default_timer()
online_algorithm_time_list.append(end - start)

def draw():
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.plot(x_values, method_of_exhaustion_time_list, c='red')
plt.plot(x_values, optimized_method_of_exhaustion_time_list, c='blue')
plt.plot(x_values, divide_and_conquer_time_list, c='orange')
plt.plot(x_values, online_algorithm_time_list, c='green')

plt.title('四种求最大子序列算法花费时间折线图')
plt.xlabel('序列的长度(2的x次方)')
plt.ylabel('花费的时间(s)')

plt.show()

ifname== 'main': bar = progressbar.ProgressBar() for i in bar(range(1, 24)): lst = generate_integer_list(2 ** i) test(lst) x_values.append(i) print('开始绘图...') draw()