PNP 算法-工具盒子

透视 n 点问题，简称 PnP，源自相机标定，是计算机视觉的经典问题，广泛应用在机器人定位、SLAM、AR/VR、摄影测量等领域。

问题定义 {#问题定义}

已知：相机的内参和畸变系数；世界坐标系中，n 个空间点坐标，以及投影在像平面上的像素坐标

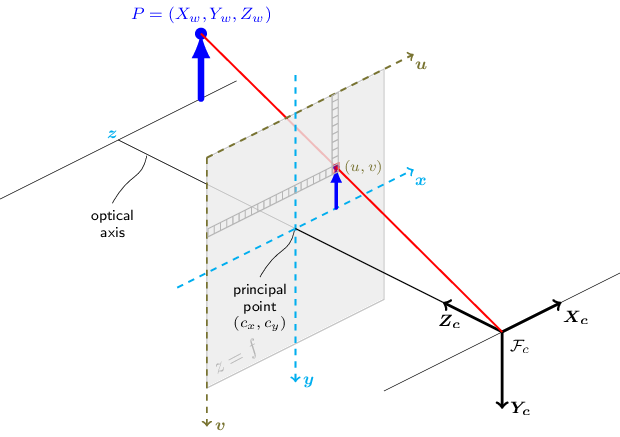
求解：相机在世界坐标系下的位姿 R 和 t，即 {W} 到 {C} 的变换矩阵 $^w_cT$，如下图：

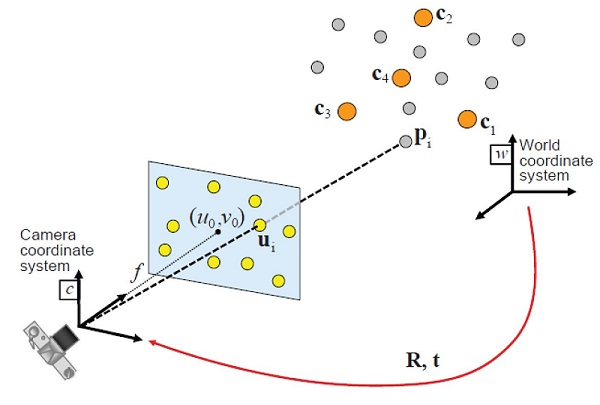
世界坐标系中的 3d 空间点，与投影到像平面的 2d 像素点，两者之间的关系为： $$ s\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}f_x&0&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix}\begin{bmatrix}r_{11}&r_{12}&r_{13}&t_1\\r_{21}&r_{22}&r_{23}&t_2\\r_{31}&r_{32}&r_{33}&t_3\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix} $$

分类 {#分类}

根据给定空间点的数量，可将 PnP 问题分为两类：

第一类 $3≤n≤5$，选取的空间点较少，可通过联立方程组的方式求解，精度易受图像噪声影响，鲁棒性较差
第二类 $n≥6$，选取的空间点较多，可转化为求解超定方程的问题，一般侧重于鲁棒性和实时性的平衡

DLT 法 {#DLT-法}

转化为 Ax=0 {#转化为-Ax-0}

令 $?=?[??]$，$K$ 为相机内参矩阵，则 PnP 问题可简化为：已知 n 组 3d-2d 对应点，求解 $P_{3×4}$

DLT (Direct Linear Transformation，直接线性变换)，便是直接利用这 n 组对应点，构建线性方程组来求解 $$ s\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}p_{11}&p_{12}&p_{13}&p_{14}\\p_{21}&p_{22}&p_{23}&p_{23}\\p_{31}&p_{32}&p_{33}&p_{33}\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\Z_w\\1\end{bmatrix} $$

简化符号 $X_w,Y_w,Z_w$ 为 $X,Y,Z$，展开得： $$ \left.\left\{\begin{array}{l}su=p_{11}X+p_{12}Y+p_{13}Z+p_{14}\\\\sv=p_{21}X+p_{22}Y+p_{23}Z+p_{24}\\\\s=p_{31}X+p_{32}Y+p_{33}Z+p_{34}\end{array}\right.\right.=>\left\{\begin{array}{l}Xp_{11}+Yp_{12}+Zp_{13}+p_{14}-uXp_{31}-uYp_{32}-uZp_{33}-up_{34}=0\\\\Xp_{21}+Yp_{22}+Zp_{23}+p_{24}-vXp_{31}-vYp_{32}-vZp_{33}-vp_{34}=0\end{array}\right. $$

未知数有 11 个 ($p_{34}$可约掉)，则至少需要 6 组对应点，写成矩阵形式如下： $$ \begin{bmatrix}X_1&Y_1&Z_1&1&0&0&0&0&-u_1X_1&-u_1Y_1&-u_1Z_1&-u_1\\0&0&0&0&X_1&Y_1&Z_1&1&-v_1X_1&-v_1Y_1&-v_1Z_1&-v_1\\\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\X_n&Y_n&Z_n&1&0&0&0&0&-u_nX_n&-u_nY_1&-u_nZ_n&-u_n\\0&0&0&0&X_n&Y_n&Z_n&1&-v_nX_n&-v_nY_n&-v_nZ_n&-v_n\end{bmatrix}\begin{bmatrix}p_{11}\\p_{12}\\p_{13}\\p_{14}\\\vdots\\p_{32}\\p_{33}\\p_{34}\end{bmatrix}=\begin{bmatrix}0\\\vdots\\\vdots\\\vdots\\0\end{bmatrix} $$

因此，求解 $?_{3×4}$ 便转化成了 $Ax=0$ 的问题

SVD 求 R t {#SVD-求-R-t}

给定相机内参矩阵 $K$，则有 $K[R|t]=λ[p_1 \text{ }p_2 \text{ }p_3\text{ }p_4]$

考虑 $λ$ 符号无关，得 $??=?^{−1}[?_1\text{ }?_2\text{ }?_3]$

SVD 分解: $$ K^{-1}\left[\begin{matrix}p_1&p_2&p_3\end{matrix}\right]=\boldsymbol{U}\begin{bmatrix}d_{11}&&&\\&d_{22}&&\\&&&d_{33}\end{bmatrix}\boldsymbol{V}^T $$ 得到： $$ \lambda\approx d_{11}\text{ 和 }\begin{cases}R=UV^T\\t=\frac{K^{-1}p_4}{d_{11}}\end{cases} $$

P3P 法 {#P3P-法}

当 n=3 时，PnP 即为 P3P，它有 4 个可能的解，求解方法是余弦定理 + 向量点积

余弦定理 {#余弦定理}

根据投影几何的消隐点和消隐线，构建 3d-2d 之间的几何关系，如下：

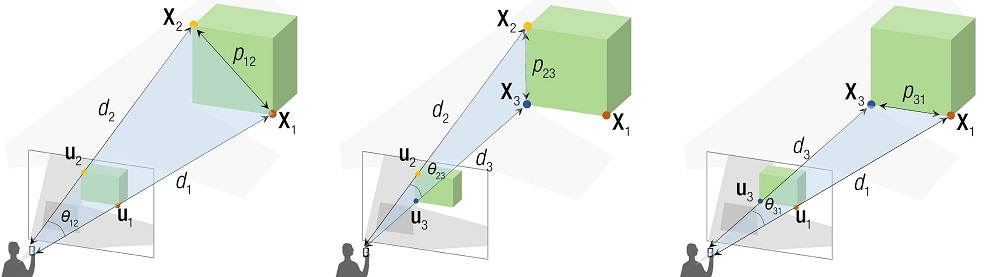
根据余弦定理，有： $$ \left.\left\{\begin{array}{l}d_1^2+d_2^2-2d_1d_2\cos\theta_{12}=p_{12}^2\\\\d_2^2+d_3^2-2d_2d_3\cos\theta_{23}=p_{23}^2\\\\d_3^2+d_1^2+2d_3d_2\cos\theta_23=p_{31}^2\end{array}\right.\right. $$

只有 $d_1,d_2,d_3$ 是未知数，求解方程组即可

其中，有个关键的隐含点：给定相机内参，以及 3d-2d 的投影关系，则消隐线之间的夹角 $θ_{12}\text{ }θ_{23}\text{ }θ_{31}$ 是可计算得出的

向量点积 {#向量点积}

相机坐标系中，原点即为消隐点，原点到 3d-2d 的连线即为消隐线，如图所示：

如果知道 3d点投影到像平面的 2d点，在相机坐标系中的坐标 $U_1,U_2,U_3$，则: $$ \cos\theta_{23}=\frac{\overrightarrow{OU_{2}}\cdot\overrightarrow{OU_{3}}}{||\overrightarrow{OU_{2}}|| ||\overrightarrow{OU_{3}}||} $$

具体到运算，可视为世界坐标系 {W} 和相机坐标系 {C} 重合，且 $Z=f$，则有: $$ [ R\quad t ]=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\end{bmatrix}=> s\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}f_x&0&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix}\begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix} $$

$K^{−1}$ 可用增广矩阵求得，且 $Z_c=f$，则有: $$ \begin{bmatrix}X_c\\Y_c\\f\end{bmatrix}=sK^{-1}\begin{bmatrix}u\\v\\1\end{bmatrix} $$ 记 $\vec{u}=\begin{bmatrix}X_c\\Y_c\\Z_c\end{bmatrix}$ , 则: $$ \cos\theta_{12}=\frac{(K^{-1}\vec{u_1})^T(K^{-1}\vec{u_2})}{||K^{-1}\vec{u_1}|| ||K^{-1}\vec{u_2}||} $$

以此类推 $\cos\theta_{23}$ 和 $\cos\theta_{31}$