聚类或聚类分析是无监督学习问题, 常被用于数据分析,本文记录聚类问题定义,以及常用聚类算法和实现。
聚类 {#聚类}
聚类分析,即聚类,是一项无监督的机器学习任务。它包括自动发现数据中的自然分组。与监督学习(类似预测建模)不同,聚类算法只解释输入数据,并在特征空间中找到自然组或群集。
聚类技术适用于没有要预测的类,而是将实例划分为自然组的情况。
---源自:《数据挖掘页:实用机器学习工具和技术》2016年。
群集通常是特征空间中的密度区域,其中来自域的示例(观测或数据行)比其他群集更接近群集。群集可以具有作为样本或点特征空间的中心(质心),并且可以具有边界或范围。
有许多类型的聚类算法。许多算法在特征空间中的示例之间使用相似度或距离度量,以发现密集的观测区域。因此,在使用聚类算法之前,扩展数据通常是良好的实践。
scikit-learn 库提供了一套不同的聚类算法供选择,我们就以 skikit-learn 库的算法为例列举常用聚类算法与相应实践。
环境配置 {#环境配置}
-
需要安装 Anaconda
-
安装 sklearn 库
聚类数据集 {#聚类数据集}
我们将使用 python sk-learn 库中的方法生成测试数据,这些数据是二维的,可以用散点图绘制数据。
引入库 {#引入库}
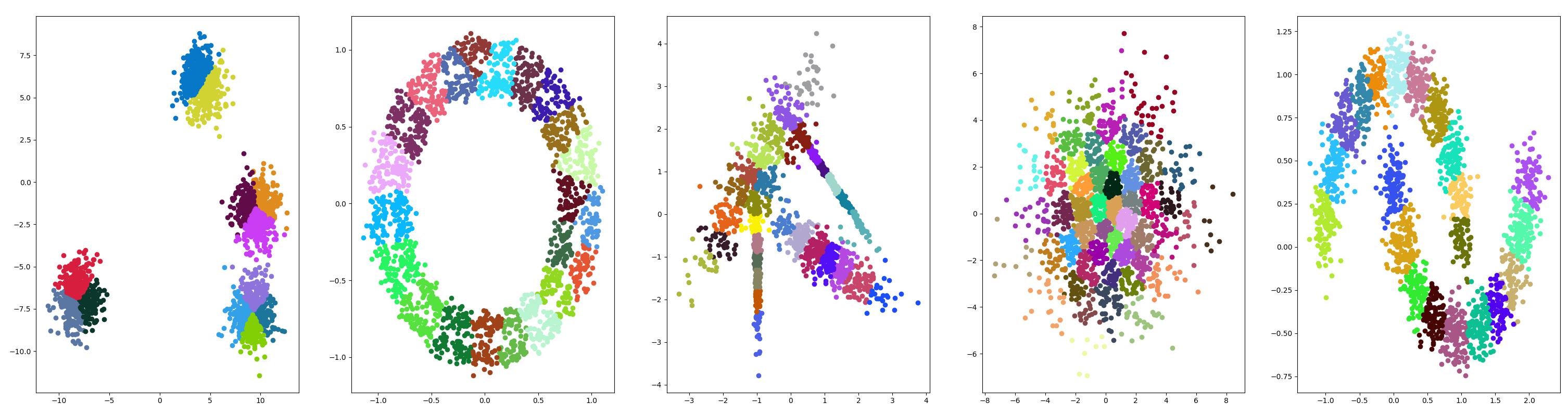
Blobs {#Blobs}
生成代码:
Moons {#Moons}
生成代码:
Circles {#Circles}
生成代码:
Classifications {#Classifications}
生成代码:
GaussianQuantiles {#GaussianQuantiles}
生成代码:
聚类算法 {#聚类算法}
亲和力传播 {#亲和力传播}
通过 AffinityPropagation 类实现的,要调整的主要配置是将" 阻尼 "设置为0.5到1 。
原理简介 {#原理简介}
亲和力传播(Affinity Propagation)是一种基于图论的聚类算法,它不需要预先指定簇的数量,并且可以发现任意形状的聚类。
亲和力传播算法的基本思想是通过计算数据点之间的"亲和力"(affinity),来确定哪些点应当属于同一个聚类。具体来说,算法的实现步骤如下:
-
初始化相似性矩阵S,其中S(i,j)表示第i个样本点与第j个样本点之间的相似度。
-
初始化责任矩阵R和可用性矩阵A,其中R(i,k)表示第i个样本点选择第k个样本点作为代表时的"责任",而A(i,k)表示第i个样本点接受第k个样本点作为代表时的"可用性"。
-
迭代更新责任矩阵R和可用性矩阵A,直到收敛为止。在每次迭代中,根据以下公式更新R和A:
R(i,k) = S(i,k) - max{A(i,k')+S(i,k')}(k'!=k)
A(i,k) = min{0, R(k,k) + sum{max(0,R(i',k))}(i'!=i,k'=1···K),其中K为样本点的数目。
-
根据最终的责任矩阵R和可用性矩阵A,确定每个样本点的聚类标签。
在亲和力传播算法中,相似性矩阵S用于描述数据点之间的相似度,而责任矩阵R和可用性矩阵A则用于计算数据点之间的"亲和力"。最终,聚类的数量由矩阵R和A中的非零元素个数决定,而每个数据点被分配到的聚类由其所对应的最大值索引确定。
需要注意的是,亲和力传播算法可能会出现收敛到局部最优解的情况,因此通常需要进行多次实验并取平均结果才能得到较为准确的聚类结果。
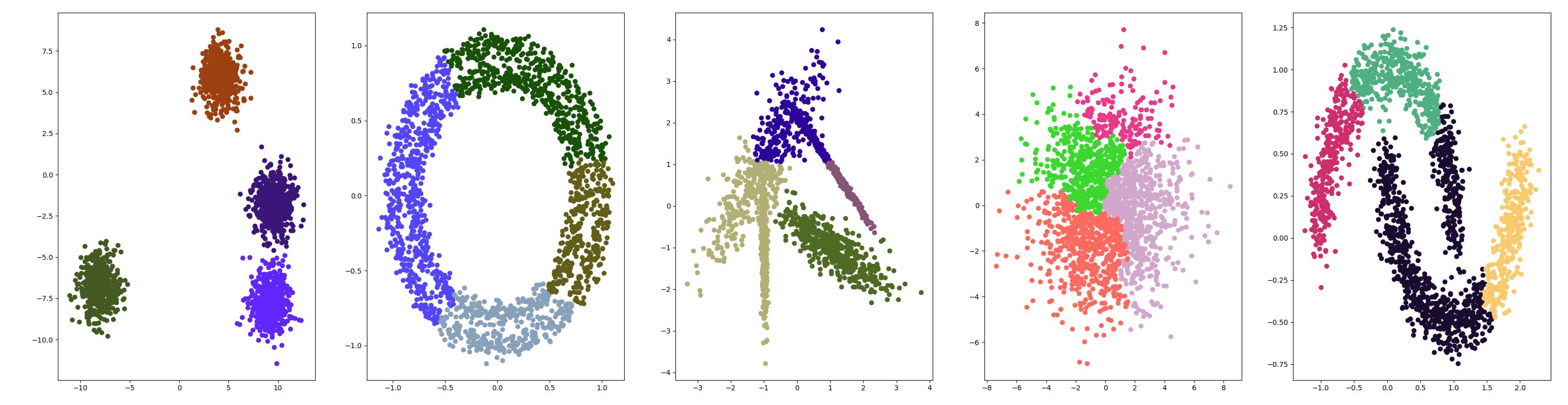
示例代码 {#示例代码}
测试结果 {#测试结果}
聚合聚类 {#聚合聚类}
聚合聚类涉及合并示例,直到达到所需的群集数量为止。它是层次聚类方法的更广泛类的一部分,通过 AgglomerationClustering 类实现的,主要配置是 n_clusters 数量,这是对数据中的群集数量的估计。
算法原理 {#算法原理}
聚合聚类是一种层次聚类方法,其原理如下:
- 初始化:将每个数据点看作一个簇。
- 计算距离:计算任意两个簇之间的距离,常用的有单链接、完全链接、平均链接等方式。这里以单链接为例,即两个簇之间的距离定义为它们中距离最近的两个数据点之间的距离。
- 合并簇:找到距离最近的两个簇,并将它们合并成一个新的簇。
- 更新距离:更新新簇与其他簇之间的距离。
- 重复步骤3和步骤4,直到所有数据点都被合并为一个簇,或者达到预设的簇数目。
- 得到聚类结果:根据聚合过程中的簇的合并情况,可以构建一棵树状图,称为聚类树或者谱系图。可以通过设置阈值来切割聚类树,得到不同的聚类结果。
聚合聚类的优点是易于实现和解释,适用于处理大规模数据集,并且可以灵活地处理不同形状和大小的簇。缺点是合并簇的顺序对最终结果有很大影响,而且需要计算任意两个簇之间的距离,运算量较大,当数据量很大时,效率可能会受到影响。此外,聚合聚类不适用于处理噪声点或者异常值。
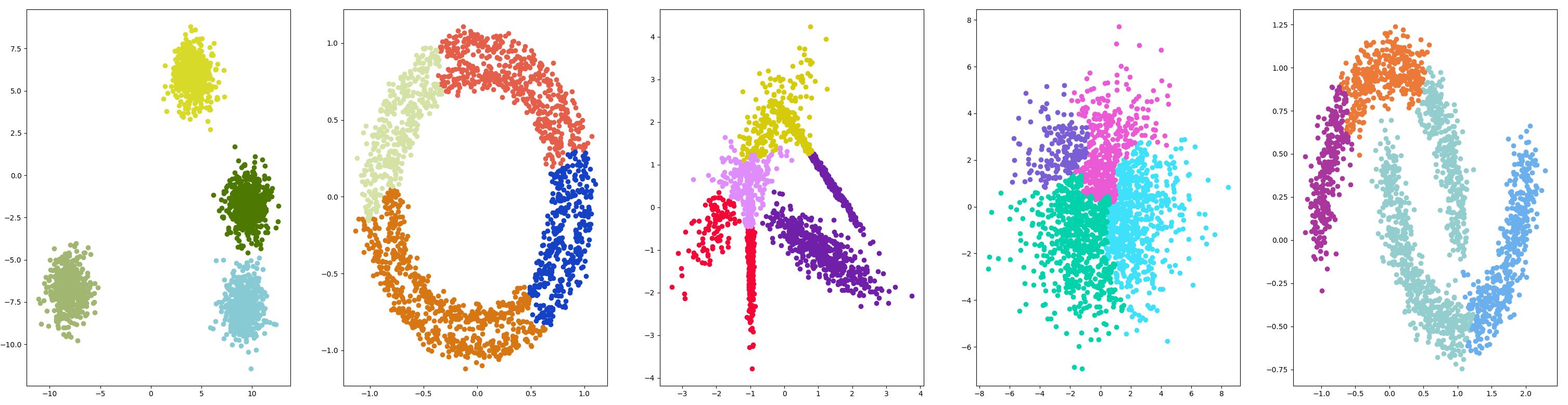
示例代码 {#示例代码-2}
以 4 类为例。
测试结果 {#测试结果-2}
BIRCH {#BIRCH}
BIRCH 聚类( BIRCH 是平衡迭代减少的缩写,聚类使用层次结构)包括构造一个树状结构,从中提取聚类质心。
示例代码 {#示例代码-3}
测试结果 {#测试结果-3}
DBSCAN {#DBSCAN}
DBSCAN 聚类(其中 DBSCAN 是基于密度的空间聚类的噪声应用程序)涉及在域中寻找高密度区域,并将其周围的特征空间区域扩展为群集。
算法原理 {#算法原理-2}
DBSCAN是一种基于密度的聚类算法,它可以将数据点划分为不同的簇,同时还可以检测出离群点。相对于其他聚类算法,如K-Means和层次聚类等,DBSCAN无需预先指定簇的数量,因此更加灵活。
DBSCAN算法的使用步骤如下:
- 确定两个参数:半径®和邻居数(minPts)。其中,半径指的是一个样本点周围的距离范围,而邻居数指的是在这个距离范围内必须至少存在的样本点数目。
- 以任意一个未访问过的数据点为起点,探索其r邻域内的所有点,如果该邻域内的点数大于或等于minPts,则将其标记为核心点(core point),否则标记为噪声点(noise point)。
- 对于每一个核心点,将其r邻域内的所有点都加入到同一个簇中,直到所有与该核心点密度可达(density-reachable)的点被访问。
- 重复上述步骤,直到所有点都被访问完成。
需要注意的是,由于DBSCAN算法是基于密度的,因此对于密度较低的区域,可能会出现无法形成簇的情况。此时,这些点将被标记为噪声点。
示例代码 {#示例代码-4}
测试结果 {#测试结果-4}
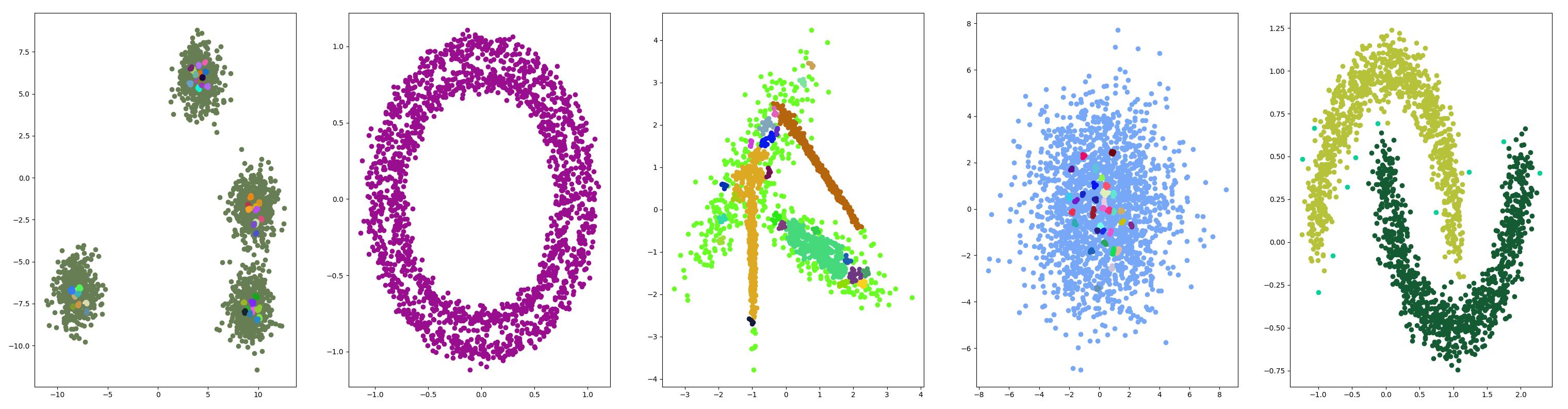
K均值 {#K均值}
K-均值聚类可以是常见的聚类算法,并涉及向群集分配示例,以尽量减少每个群集内的方差。
算法原理 {#算法原理-3}
K-means算法是一种常用的聚类算法,其基本思想是将样本点划分为K个簇,使簇内的数据点相似度较高,而簇间的数据点相似度较低。
具体来说,K-means算法的实现步骤如下:
- 随机选择K个点作为簇心(cluster centers)。
- 对剩余的每个点计算距离,将其归为距离最近的簇心所在的簇。
- 重新计算每个簇的簇心。
- 重复上述步骤,直到满足停止条件为止。停止条件可以是达到预定的迭代次数,或者簇心不再发生变化。
需要注意的是,在K-means算法中,初始簇心的选择对最终结果有很大的影响。不同的初始簇心可能会导致不同的聚类结果,因此通常采用多次随机初始化的方法来获取较为稳定的聚类结果。
此外,K-means算法还有一些优化技巧,例如 k-means++ 初始化方法和 Mini Batch K-Means 等,这些优化方法可以提高算法的速度和精度。
示例代码 {#示例代码-5}
测试结果 {#测试结果-5}
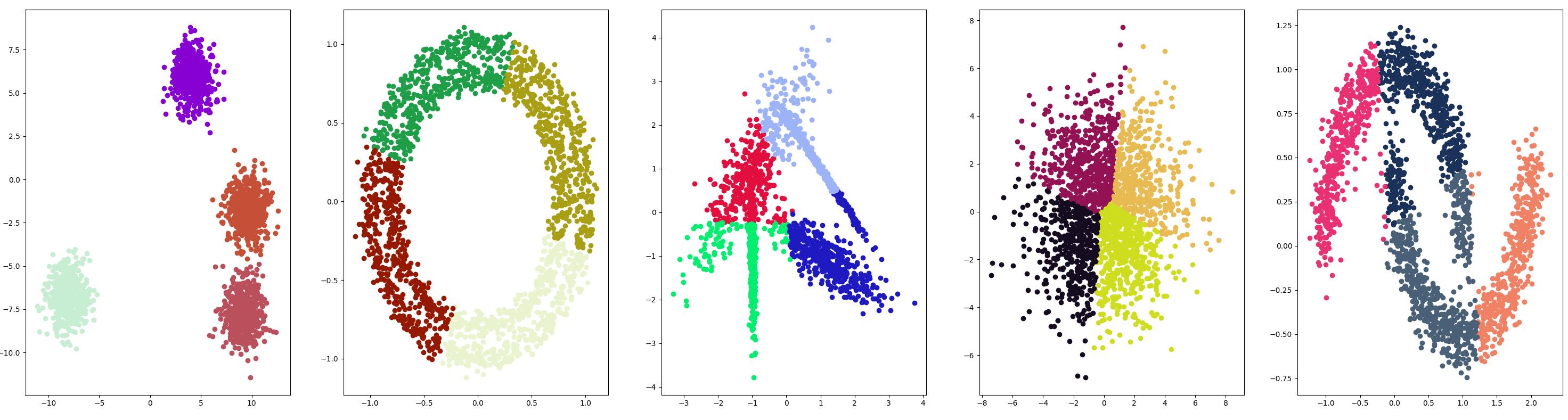
Mini-Batch K-均值 {#Mini-Batch-K-均值}
Mini-Batch K-均值是 K-均值的修改版本,它使用小批量的样本而不是整个数据集对群集质心进行更新,这可以使大数据集的更新速度更快,并且可能对统计噪声更健壮。
算法原理 {#算法原理-4}
Mini Batch K-Means 算法是 K-Means 算法的一种优化方法,它可以加快算法的收敛速度,并且在处理大规模数据时比传统K-Means算法更加高效。
Mini Batch K-Means算法的基本原理如下:
- 随机选择k个点作为初始簇心。
- 从数据集中随机选择一小部分样本(称为mini-batch),并将其用于更新簇心。具体来说,对于每个mini-batch中的样本,根据其距离最近的簇心,将其划分到相应的簇中,并重新计算该簇的簇心。
- 重复进行第2步,直到满足停止条件为止。通常情况下,停止条件可以是达到预定的迭代次数,或者簇心不再发生变化。
相比于传统的K-Means算法,Mini Batch K-Means算法的优势在于可以通过选择较小的mini-batch来加速算法的收敛过程。此外,Mini Batch K-Means还可以减少内存使用量,并且可以适应在线学习的场景。
需要注意的是,由于Mini Batch K-Means是一种随机采样的算法,因此可能会导致聚类结果的稳定性略有降低。对于某些数据集,可能需要进行多次实验并取平均结果才能得到较为准确的聚类结果。
示例代码 {#示例代码-6}
测试结果 {#测试结果-6}
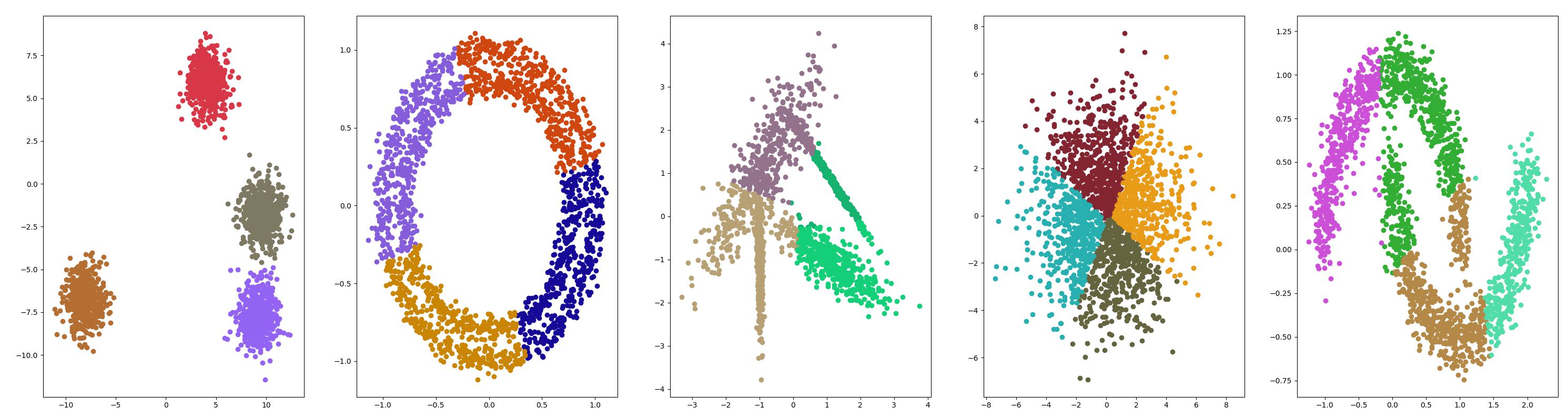
均值漂移聚类 {#均值漂移聚类}
均值漂移聚类涉及到根据特征空间中的实例密度来寻找和调整质心。
算法原理 {#算法原理-5}
Mean Shift算法是一种基于密度估计的非参数聚类算法,其可以自动确定聚类的数量,并且对不同形状的聚类效果良好。
Mean Shift算法的基本思想是通过不断移动数据点(或者簇心),直到达到局部密度最大的位置为止。具体来说,算法的实现步骤如下:
- 随机选择一个数据点作为起始点。
- 定义一个圆形窗口(可以是高斯核函数),并以该点为中心进行滑动。
- 计算圆形窗口内所有点的重心(即平均值),将当前点向该重心方向移动。
- 重复步骤2和步骤3,直到不再有新的数据点落在圆形窗口内为止。
- 将最终停留在同一个位置的数据点归为同一个簇。
需要注意的是,Mean Shift算法在每个迭代过程中都会按照密度最大化的原则移动数据点,因此可以获得相对较好的聚类效果。但是由于算法的计算复杂度较高,在处理大规模数据时可能会出现性能瓶颈。此外,算法的参数设置也会影响聚类结果,例如窗口大小和核函数选择等。
示例代码 {#示例代码-7}
测试结果 {#测试结果-7}
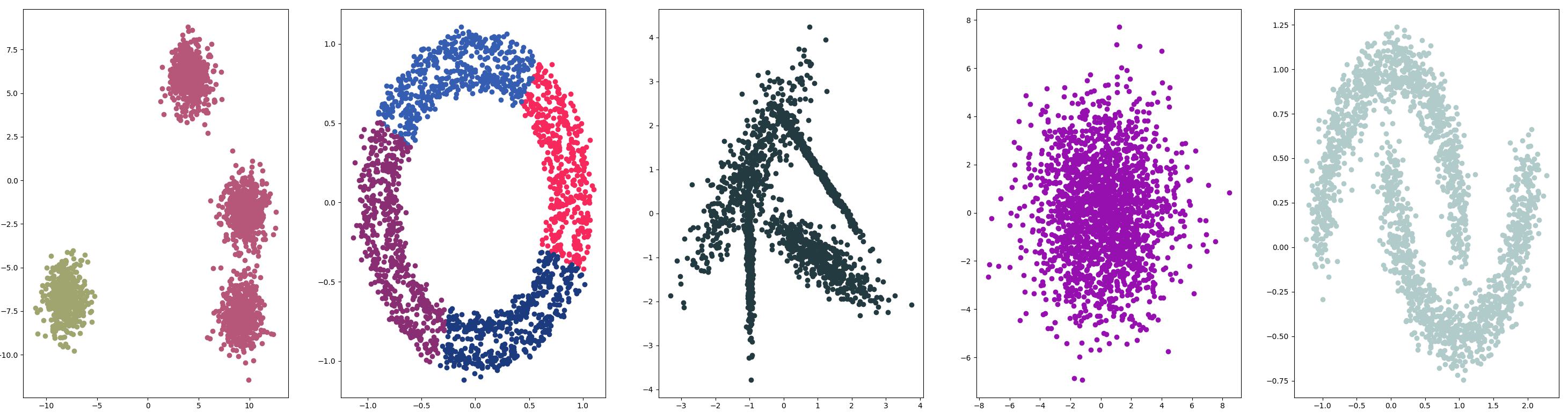
OPTICS {#OPTICS}
OPTICS 聚是上述 DBSCAN 的修改版本。
算法原理 {#算法原理-6}
OPTICS(Ordering Points To Identify the Clustering Structure)算法是一种基于密度的聚类算法,它可以处理任意形状的聚类,并且不需要指定簇的数量。
OPTICS算法的基本思想是通过计算数据点的"可达距离"(reachability distance),来确定数据点之间的聚类关系。具体来说,算法的实现步骤如下:
- 对每个数据点计算其与周围其他点之间的距离。根据一个距离参数ε,将所有距离小于ε的点归为同一个邻域。
- 对每个点计算其核心距离(core distance),即其邻域中第k个最远的点与该点的距离,其中k为用户事先指定的参数。
- 对每个点计算其可达距离(reachability distance),即其到核心距离更大的某个点之间的最短距离,或者定义为无穷大表示不可达。
- 对所有点按照可达距离从小到大排序,构建一个"可达距离图"。
- 根据可达距离图,确定每个点的聚类标签。具体来说,从图中一个未被访问的点开始,向下搜索所有可达的点,并将其归为同一簇。如果找到一个可达距离较小的点,则将当前簇中的点分为两个子簇,并继续搜索下一个未被访问的点。
需要注意的是,OPTICS算法的性能与参数设置(特别是ε和k)有很大关系。对于不同的数据集,可能需要进行多次实验来确定最佳的参数值。此外,由于算法的时间复杂度较高,在处理大规模数据时可能会出现性能瓶颈。
示例代码 {#示例代码-8}
测试结果 {#测试结果-8}
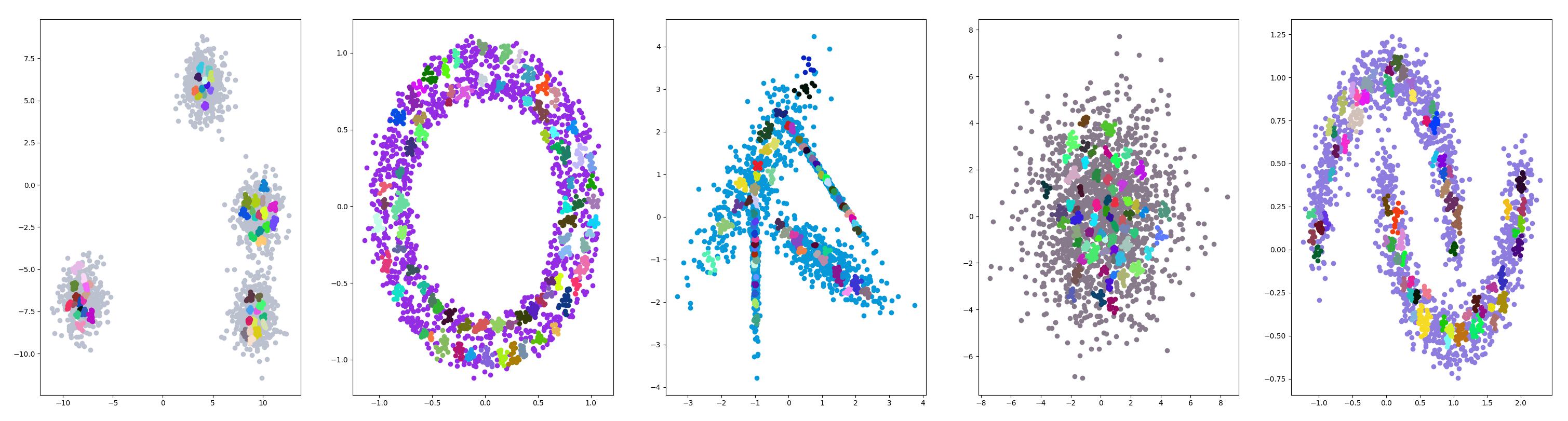
光谱聚类 {#光谱聚类}
光谱聚类是一类通用的聚类方法,取自线性线性代数。
算法原理 {#算法原理-7}
光谱聚类是一种基于数据的相似度矩阵进行聚类分析的方法,其原理如下:
- 构造相似度矩阵:首先根据某种相似度度量方法计算样本点之间的相似度,可以使用欧氏距离、余弦相似度等不同的度量方法来计算相似度。
- 降维:将相似度矩阵转换为低维空间,这一步通常使用特征值分解或者奇异值分解来实现。通过降维,可以减少计算量,提高聚类的速度和效率。
- 聚类分析:在低维空间中对样本进行聚类,常见的聚类方法包括K-means聚类、层次聚类等。
相比传统聚类方法,光谱聚类可以处理非球形、不同密度的数据,而且具有较好的可扩展性。但是,光谱聚类也有一些缺点,例如需要选择合适的相似度度量方法、降维维数以及聚类算法等参数,这些参数的选择可能会影响聚类结果的质量。
示例代码 {#示例代码-9}
测试结果 {#测试结果-9}
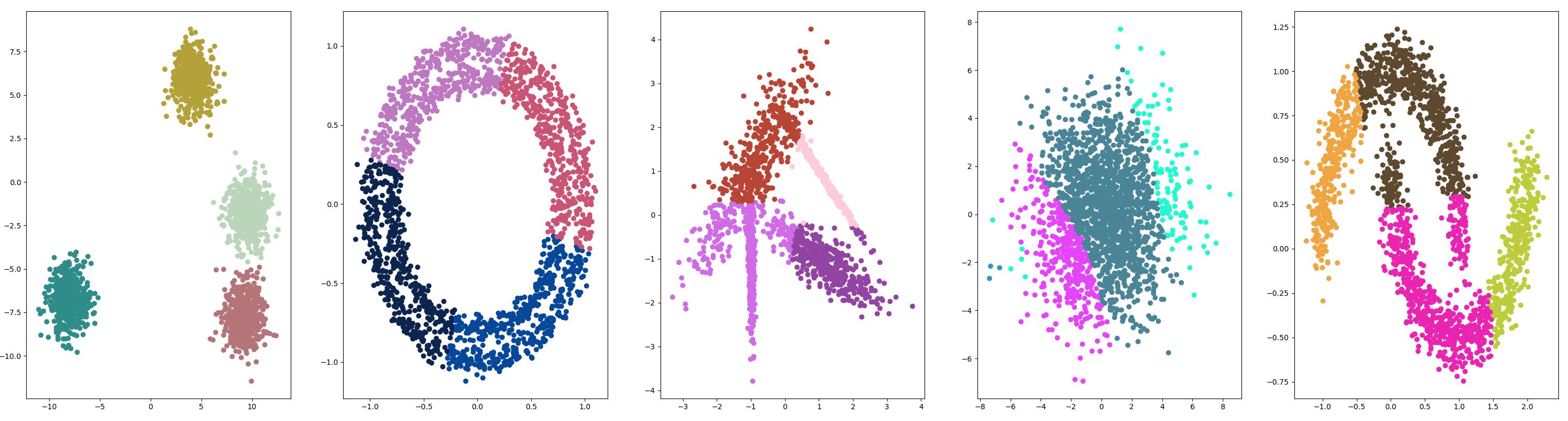
高斯混合模型 {#高斯混合模型}
高斯混合模型总结了一个多变量概率密度函数,顾名思义就是混合了高斯概率分布。它是通过 Gaussian Mixture 类实现的,要优化的主要配置是 n_clusters 超参数,用于指定数据中估计的群集数量。
算法原理 {#算法原理-8}
高斯混合模型聚类是一种基于概率密度函数进行聚类的方法,其原理如下:
- 假设每个簇服从一个高斯分布:首先,我们假设数据可以划分为若干个簇,每个簇对应一个多元高斯分布。这个假设意味着每个簇内的数据点在各个维度上的取值都符合正态分布。
- 确定模型参数:接下来,我们需要估计每个高斯分布的参数,包括均值、方差和权重。其中权重表示每个簇的占比,用来确定每个簇的重要性。
- 最大化似然函数:根据样本数据和模型参数,计算出每个数据点属于每个簇的后验概率,即给定模型参数下,该数据点属于每个簇的概率。然后,通过最大化似然函数来更新模型参数,以使得后验概率最大化。
- 迭代求解模型参数:通过迭代运算反复更新模型参数,直到收敛为止,得到最终的模型参数。
- 聚类结果:最终,根据每个数据点的后验概率进行分类,将后验概率最大的簇作为该数据点所属的簇。
高斯混合模型聚类可以处理非凸、不同形状和密度的数据,而且对噪声具有较好的鲁棒性。然而,由于需要迭代求解,运算量较大,算法的收敛速度也比较慢。此外,高斯混合模型聚类对于初始值选择和簇数的确定比较敏感,这也是需要注意的问题。
示例代码 {#示例代码-10}
测试结果 {#测试结果-10}
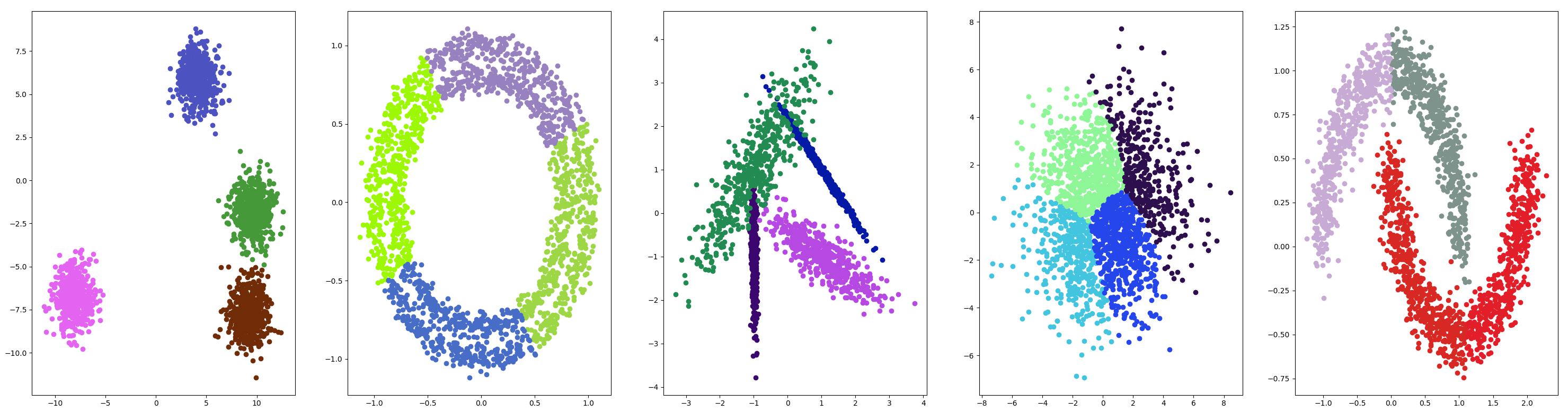
错误解决 {#错误解决}
报错:AttributeError: 'NoneType' object has no attribute 'split' {#报错:AttributeError-‘NoneType‘-object-has-no-attribute-‘split‘}
- 一般都是包依赖的问题,无脑升级一般可以解决问题:
参考资料 {#参考资料}
- https://z.itpub.net/article/detail/280D736A45F668E9743211BBF181DB52
- https://zhuanlan.zhihu.com/p/595122648
- https://www.51cto.com/article/718285.html
- https://scikitlearn.com.cn/0.21.3/47/
- https://cloud.tencent.com/developer/article/1042011
文章链接:
https://www.zywvvd.com/notes/study/algorithm/clustering/clustering/
 51工具盒子
51工具盒子