提到算法,并不陌生,很多初学者可能认为算法都是后台的事,学前端不用学算法,这是个误区。算法是程序的灵魂,一个优秀前端工程师对算法也是要需要熟练掌握的,尤其对于梦想成为一位全栈工程师,精通不在话下了。
首先我们来看张算法列表图,如下:
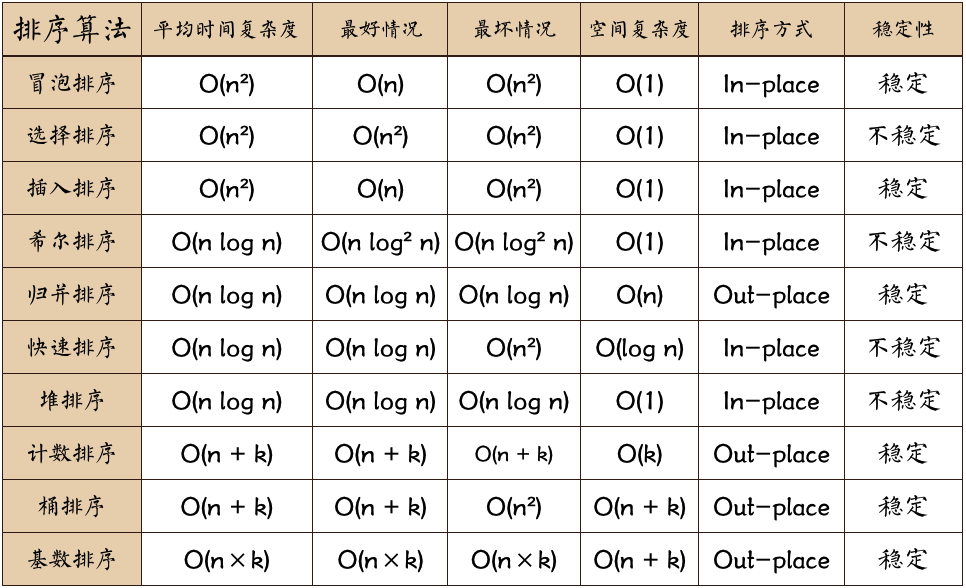
图片名词解释:
n: 数据规模;
k:"桶"的个数;
In-place: 占用常数内存,不占用额外内存;
Out-place: 占用额外内存;
接下来我们一起来了解下一些常用的算法(网络收藏)和尝试做一组面试题。
排序算法
1. 冒泡排序
这种算法不多说,有点变成基础的人都能看明白,可以说是"傻瓜排序"。
function bubbleSort(arr){
var i = j = 0;
for(i=1;i<arr.length;i++){
for(j=0;j<arr.length-i;j++){
var temp = 0;
if(arr[j]>arr[j+1]){
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
2. 快速排序
function quickSort(arr,l,r){
if(l < r){
var i = l, j = r, x = arr[i];
while(i<j){
while(i<j && arr[j]>x)
j--;
if(i<j)
//这里用i++,被换过来的必然比x小,赋值后直接让i自加,不用再比较,可以提高效率
arr[i++] = arr[j];
while(i<j && arr[i]<x)
i++;
if(i<j)
//这里用j--,被换过来的必然比x大,赋值后直接让j自减,不用再比较,可以提高效率
arr[j--] = arr[i];
}
arr[i] = x;
quickSort(arr, l, i-1);
quickSort(arr, i+1, r);
}
}
3. 二路归并
PS:将两个按值有序序列合并成一个按值有序序列,则称之为二路归并排序。
function merge(left, right) {
var result = [],
il = 0,
ir = 0;
while (il < left.length && ir < right.length) {
if (left[il] < right[ir]) {
result.push(left[il++]);
} else {
result.push(right[ir++]);
}
}
while(left[il]){
result.push(left[il++]);
}
while(right[ir]){
result.push(right[ir++]);
}
return result;
}
字符串操作
1. 判断回文字符串
function palindrome(str){
// \W匹配任何非单词字符。等价于“[^A-Za-z0-9_]”。
var re = /[\W_]/g;
// 将字符串变成小写字符,并干掉除字母数字外的字符
var lowRegStr = str.toLowerCase().replace(re,'');
// 如果字符串lowRegStr的length长度为0时,字符串即是palindrome
if(lowRegStr.length===0)
return true;
// 如果字符串的第一个和最后一个字符不相同,那么字符串就不是palindrome
if(lowRegStr[0]!=lowRegStr[lowRegStr.length-1])
return false;
//递归
return palindrome(lowRegStr.slice(1,lowRegStr.length-1));
}
2. 翻转字符串
2.1 思路1:反向遍历字符串
function reverseString(str){
var tmp = '';
for(var i=str.length-1;i>=0;i--)
tmp += str[i];
return tmp
}
2.2 思路2:转化成array操作。
function reverseString2(str){
var arr = str.split("");
var i = 0,j = arr.length-1;
while(i<j){
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
return arr.join("");
}
PS:什么?你要问为啥不直接操作str? 因为str[i]是只读的,不能str[0]=str[1]这样操作。
再PS:如果允许用reverse(),也可以用'str'.split('').reverse().join('')实现。
3. 生成指定长度随机字符串
PS:配合模糊等效果可以生成个验证码
function randomString(n){
var str = 'abcdefghijklmnopqrstuvwxyz0123456789';
var tmp = '';
for(var i=0;i<n;i++)
tmp += str.charAt(Math.round(Math.random()*str.length));
return tmp;
}
4. 统计字符串中次数最多字母
PS:利用Object中key的唯一性,利用key来进行筛选,然后计数。
function findMaxDuplicateChar(str) {
if(str.length == 1) {
return str;
}
var charObj = {};
for(var i = 0; i < str.length; i++) {
if(!charObj[str.charAt(i)]) {
charObj[str.charAt(i)] = 1;
} else {
charObj[str.charAt(i)] += 1;
}
}
var maxChar = '',
maxValue = 1;
for(var k in charObj) {
if(charObj[k] >= maxValue) {
maxChar = k;
maxValue = charObj[k];
}
}
return maxChar + ':' + maxValue;
}
数组操作
1. 数组去重
PS: 还是利用Object中key的唯一性,利用key来进行筛选。
function unique(arr){
var obj = {}
var data = []
for(var i in arr){
if(!obj[arr[i]]){
obj[arr[i]] = true;
data.push(arr[i]);
}
}
return data;
}
2. Number数组中最大差值
function getMaxProfit(arr){
var min = arr[0], max = arr[0];
for(var i=0;i<arr.length;i++){
if(arr[i]<min)
min = arr[i];
if(arr[i]>max)
max = arr[i];
}
return max - min;
}
其他常见算法
1. 阶乘
1.1 非递归实现
function factorialize(num) {
var result = 1;
if(num < 2) return 1;
while(num>1)
result *= num--;
return result;
}
1.2 递归实现
function factorialize(num) {
var result = 1;
if(num < 2) return 1;
if(num > 1){
return num * factorialize(num - 1);
}
}
2. 生成菲波那切数列
PS:斐波那契数列,又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、......在数学上,斐波纳契数列主要考察递归的调用。通过定义fibo[i] = fibo[i-1]+fibo[i-2];来生成斐波那契数组。
2.1 强行递归实现
function getfib(n){
if (n < 2) {
return n;
} else {
return getfib(n-1) + getfib(n-2);
}
}
function fibo(len){
var fibo = [];
for(var i=0;i<len;i++)
fibo.push(getfib(i));
return fibo;
}
2. 生成菲波那切数列
PS:斐波那契数列,又称黄金分割数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、......在数学上,斐波纳契数列主要考察递归的调用。通过定义fibo[i] = fibo[i-1]+fibo[i-2];来生成斐波那契数组。
2.1 强行递归实现
function getfib(n){
if (n < 2) {
return n;
} else {
return getfib(n-1) + getfib(n-2);
}
}
function fibo(len){
var fibo = [];
for(var i=0;i<len;i++)
fibo.push(getfib(i));
return fibo;
}
2.2 简约非递归版
function getFibonacci(n) {
var fibarr = [];
var i = 0;
while(i < n) {
if(i <= 1) {
fibarr.push(i);
} else {
fibarr.push(fibarr[i - 1] + fibarr[i - 2])
}
i++;
}
return fibarr;
}
3. 二分查找
PS:二分查找又称折半查找,是在有序数组查找中用到的较为频繁的一种算法,优点是比较次数少,查找速度快,平均性能好;其缺点是要求待查表为有序表,且插入删除困难。
3.1 非递归实现
function binary_search(arr, key) {
var low = 0,
high = arr.length - 1;
while(low <= high){
var mid = parseInt((high + low) / 2);
if(key == arr[mid]){
return mid;
}else if(key > arr[mid]){
low = mid + 1;
}else if(key < arr[mid]){
high = mid -1;
}
}
return -1;
};
3.2 递归实现
function binary_search2(arr, low, high, key) {
if(low > high)
return -1;
var mid = parseInt((low + high)/2);
if(key == arr[mid])
return mid;
else if(key > arr[mid])
return binary_search2(arr, mid+1, high, key);
else if(key < arr[mid])
return binary_search2(arr, low, mid-1, key);
}
了解完以上的算法,我们可以尝试下做一组关于算法的题目。我们可以点下链接:分享10道关于算法的习题
总结
算法是前后端工程师必须掌握的,加强学习吧。
 51工具盒子
51工具盒子